238. EXAMPLE If the normals at three points P, Q and R in a s be the focus, meet point O and prove that SP. SQ. SR a SO As in the previous question we know that the normals a the points (ami, am 1), (am am2) and (am3, 2am3) meet in the point (h k), if m1 1m2 1m3 0 2a -h m2m3 m3m1 m1m2 (2)

Video Solution

Text Solution

Verified by Experts

$y = m x - 2 a m - a m^{3}$
$(a m_{1}^{2}, - 2 a m_{1}) (a m_{2}^{2}, - 2 a m_{2}) (a m_{3}^{2}, - 2 a m_{3})$
$a m^{3} + 2 a m - m h + k = 0$
$m_{1} + m_{2} + m_{3} = 0$
$m_{1} m_{2} + m_{1} m_{3} + m_{2} m_{3} = \frac{2 a - h}{a}$
$m_{1} m_{2} m_{3} = - \frac{k}{a}$
=SPSQSR
$= (a m_{1}^{2} + a) (a m_{2}^{2} + a) (a m_{3}^{2} + a)$
$= a^{3} (m_{1}^{2} + 1) (m_{2}^{2} +!) (m_{3}^{2} + 1)$
$= a^{3} (m_{1}^{2} \cdot m_{2}^{2} m_{3}^{2} + m_{1}^{2} m_{2}^{2} + m_{1}^{2} m_{3}^{2} + n_{1}^{2} + m_{3}^{2} m_{3}^{2} + m_{2} + m_{3}^{2} + 1)$
$= a^{3} [\frac{h^{2} - 2 a h + a^{2}}{a^{2}}]$
$\frac{a^{3}}{a^{2}} {(h - a)}^{2}$
$a {(O S)}^{2}$ .

|

Class 12 MATHS RELATIONS AND FUNCTIONS

Similar Questions

Knowledge Check

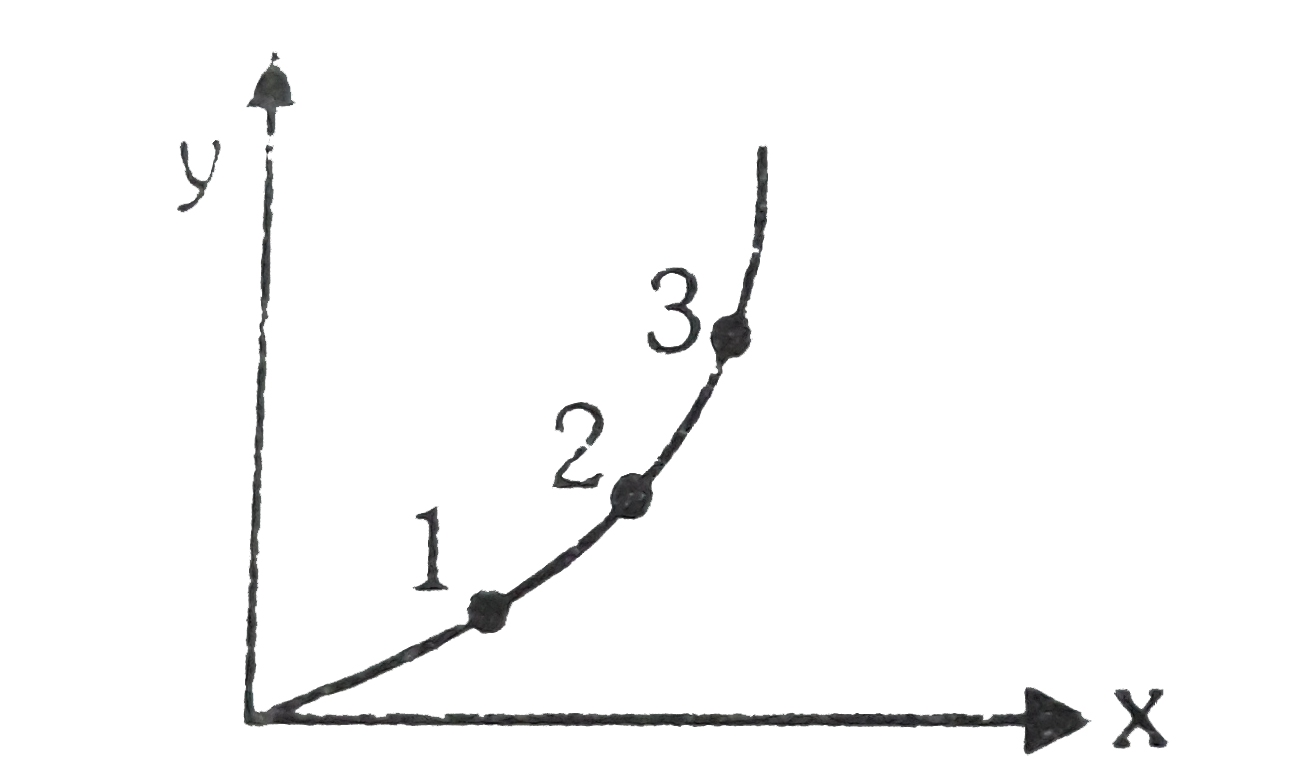
The slope of graph as shown in figure at points 1, 2 and 3 is $m_{1}, m_{2} and m_{3}$ respectively then

A $m_{1} > m_{2} > m_{3}$
B $m_{1} < m_{2} < m_{3}$
C $m_{1} = m_{2} = m_{3}$
D $m_{1} = m_{3} > m_{2}$

Recommended Questions

Home
Ask Doubt
Profile