A block is placed on a ramp of parabolic shape given by the equation y=x2/20 , sec Figure.

If μs=0.5 , what is the maximum height above the ground at which the block can be placed without slipping ?
(tanθ=μs=dydx)
For the body not to drop
mg cosθ=μmgsinθ
⇒tanθ=μ given μ=0.5
But tanθ=dydx slpoe of parabolic region
⇒dydx=μ=0.5 .......(1)
given y=x220∴dydx=2x20=x10 ....(2)
∴ slope yx=0.5⇒0.5=x10⇒x=5 ...(3)
From eq . (1) & (3) vertical height ,
y=x220=5×520=1.25m
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - LAWA OF MOTIONEXERCISE - ADDITIONAL PROBLEMS22videos
LAWA OF MOTION
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - KINETIC THEORYEXERCISE - Additional Problems5videos
KINETIC THEORY
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - LAWS OF MOTIONEXERCISE - LONG ANSWER QUESTIONS3videos
LAWS OF MOTION
Similar Questions
A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
View SolutionA block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
A(a) 16mB(b) 23mC(c) 13mD(d) 12m - Question 2 - Select One
A block of mass m is placed on a surface with a vertical cross section given by y=x3/6. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is :
A1/2mB16mC2/3D1/3m - Question 3 - Select One
A parabolic bow1 with its bottom at origin has the shape y=x220 where x and y are in metre The maximum height at which a small mass m can be placed on the bowl without slipping is (coeff of static friction 0.5
 .A1.25NmB2.5mC1.0mD4.0m
.A1.25NmB2.5mC1.0mD4.0m
A block of mass 'm' is placed on a rough surface with a vertical cross section of y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is .
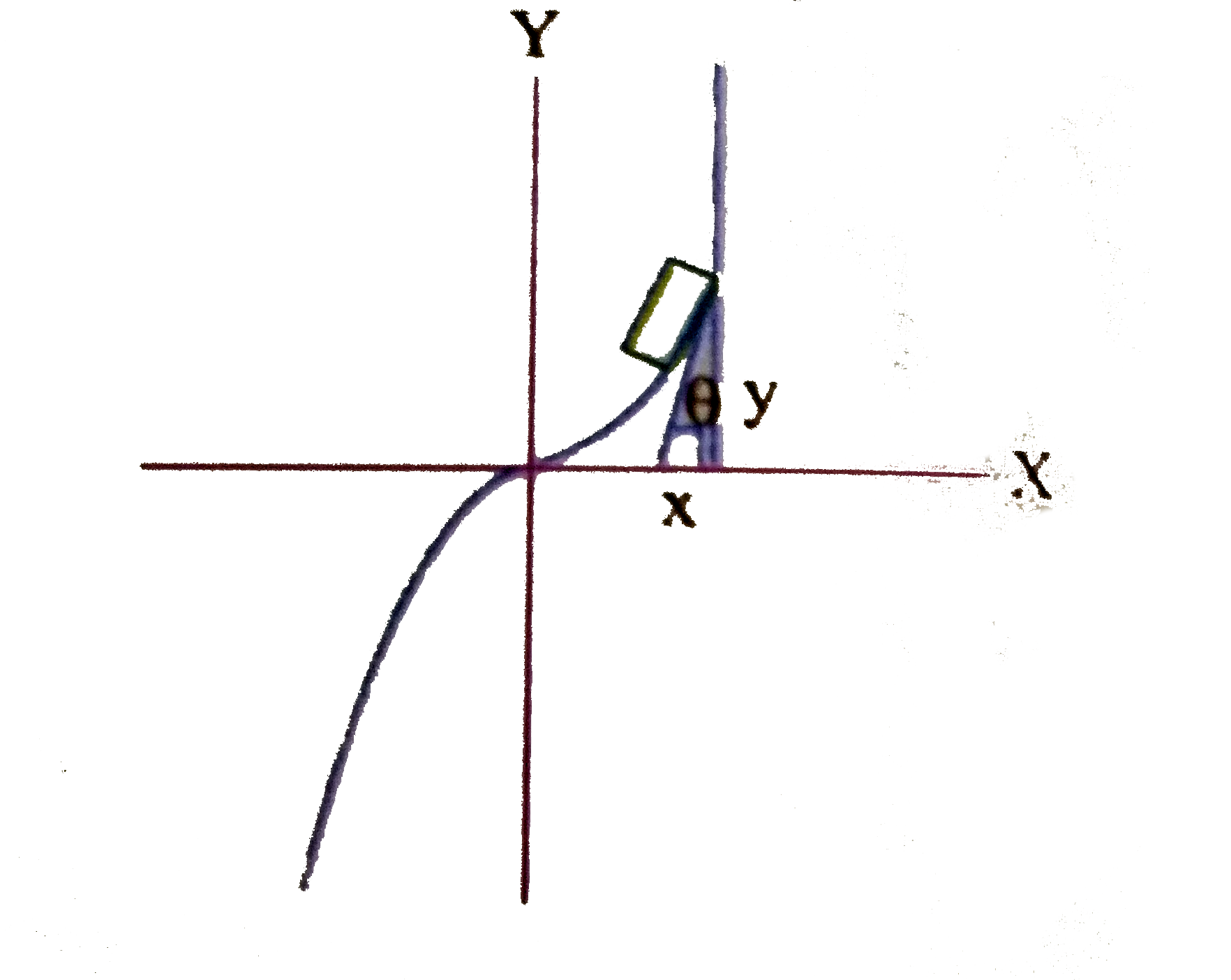 View Solution
View SolutionA block of mass m is palced on a surface having coefficient of frictionn 0.25, with a vertical cross section given by y=x416. Calculate the maximum height above the ground t which block can be placed without slipping.
View SolutionA disc of radius 5 m is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
View SolutionA parabolic bow1 with its bottom at origin has the shape y=x220 where x and y are in metre The maximum height at which a small mass m can be placed on the bowl without slipping is (coeff of static friction 0.5
 .View Solution
.View SolutionA disc of radius is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
View Solution

