A 50 turns circular coil has a radius of 3cm , it is kept in a magnetic field acting normal to the area of the coil. The magnetic field B increased from 0.10 tesla to 0.35 tesla in 2 milliseconds . The average induced e.m.f. in the coil is
1.77volts
17.7volts
177volts
0.177volts
The correct Answer is:B
To solve the problem of finding the average induced e.m.f. in a circular coil when the magnetic field changes, we can follow these steps:
Step 1: Identify the given values
- Number of turns (N) = 50
- Radius of the coil (r) = 3 cm = 0.03 m (convert to meters)
- Initial magnetic field (B1) = 0.10 T
- Final magnetic field (B2) = 0.35 T
- Time interval (t) = 2 ms = 2 × 10^(-3) s (convert to seconds)
Step 2: Calculate the area of the coil
The area (A) of a circular coil can be calculated using the formula:
A=πr2
Substituting the radius:
A=π(0.03)2
A=π(0.0009)
A≈0.002827m2
Step 3: Calculate the change in magnetic flux
The magnetic flux (Φ) through the coil is given by:
Φ=N⋅B⋅A
- For initial flux (Φ1):
Φ1=N⋅B1⋅A=50⋅0.10⋅0.002827
Φ1≈0.14135Wb
- For final flux (Φ2):
Φ2=N⋅B2⋅A=50⋅0.35⋅0.002827
Φ2≈0.24745Wb
Step 4: Calculate the change in magnetic flux
The change in magnetic flux (ΔΦ) is:
ΔΦ=Φ2−Φ1
ΔΦ≈0.24745−0.14135
ΔΦ≈0.1061Wb
Step 5: Calculate the average induced e.m.f.
The average induced e.m.f. (E) can be calculated using Faraday's law:
E=ΔΦΔt
Substituting the values:
E=0.10612×10−3
E≈53.05V
Step 6: Finalize the answer
The average induced e.m.f. in the coil is approximately 53.05 V.
- Number of turns (N) = 50
- Radius of the coil (r) = 3 cm = 0.03 m (convert to meters)
- Initial magnetic field (B1) = 0.10 T
- Final magnetic field (B2) = 0.35 T
- Time interval (t) = 2 ms = 2 × 10^(-3) s (convert to seconds)
The area (A) of a circular coil can be calculated using the formula:
A=πr2
Substituting the radius:
A=π(0.03)2
A=π(0.0009)
A≈0.002827m2
The magnetic flux (Φ) through the coil is given by:
Φ=N⋅B⋅A
- For initial flux (Φ1):
Φ1=N⋅B1⋅A=50⋅0.10⋅0.002827
Φ1≈0.14135Wb
Φ2=N⋅B2⋅A=50⋅0.35⋅0.002827
Φ2≈0.24745Wb
The change in magnetic flux (ΔΦ) is:
ΔΦ=Φ2−Φ1
ΔΦ≈0.24745−0.14135
ΔΦ≈0.1061Wb
The average induced e.m.f. (E) can be calculated using Faraday's law:
E=ΔΦΔt
Substituting the values:
E=0.10612×10−3
E≈53.05V
The average induced e.m.f. in the coil is approximately 53.05 V.
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - ERRORLESS CHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - OT
3 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - ERRORLESS CHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Motional EMI
1 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Self Evaluation Test -19
23 Videos
- ELECTRON, PHOTON, PHOTOELECTRIC EFFECT AND X-RAYSBOOK - ERRORLESS CHAPTER - ELECTRON, PHOTON, PHOTOELECTRIC EFFECT AND X-RAYSEXERCISE - Self Evaluation Test
3 Videos
Similar Questions
A circular coil of 20 turns and radius 10cm is placed in uniform magnetic field of 0.10T normal to the plane of the coil.If the current coil is 5A ,then the torque acting on the coil will be: ?
View SolutionA circular coil of 20 turns and radius 10 cin is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, the total torque on the coil will be
View Solution
Knowledge Check
A circular coil of radius r is placed in a uniform magnetic field B. The magnetic field is normal to the plane of the coil is rotated at an angular speed of ω, about its own axis , then the induced emf in the coil is __
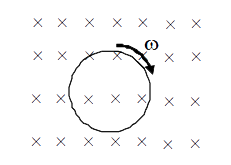 ABAω2πBB(2πr)ωC0Dnone of the above
ABAω2πBB(2πr)ωC0Dnone of the aboveA circular coil of 20 turns and radius 10 cm is placed in uniform magnetic field of 0.10T normal to the plane of the coil. If the current in coil is 5A, then the torque acting on the coil will be
A31.4NmB3.14NmC0.314NmDZeroA coil of area 0.4m2 has 100 turns. A magnetic field of 0.04Wb/m−2 is acting normal to the coil surface. If this magnetic field is reduced to zero in 0.01 s, then the induced emf in the coil is
A160VB250 VC270 VD320 V
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
View SolutionA circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
View SolutionThe magnetic field in a coil of 100 turns and 40 square cm area is increased from 1 Tesla to 6 Tesla in 2 second. The magnetic field is perpendicular to the coil. The e.m.f. generated in it is
View SolutionThe radius of a circular coil having 100 turns is 5 cm .its plane is normal to the magnetic field. The magnetic field changes from 2T to 10 T in 3.14 sec. The induced emf in coil will be
View SolutionA circular coil of 25 turns and radius of 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of coil. If the current in the coil is 5 A, then total torque experienced by the coil is
View Solution
