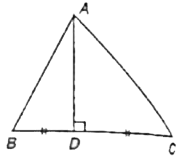
In the adjoining figure AB= AC and D is the mid-point of BC. Use SSS rule of congruency to show that △ABD≅△ACD AD is bisector of ∠A AD is perpendicular to BC
In∠ABDand∠ACD
AB=AC(GIVEN)
BD=DC(D is mid point of BC)
AD=AD
so,∠ABD≅∠ACD
so, ∠BAD=∠CAD
and∠ADB=∠ADC=180o2=90o
this means AD is perpendicular BC
Similar Questions
In the adjoining figure AB= AC and D is the mid-point of BC. Use SSS rule of congruency to show that △ABD≅△ACD AD is bisector of ∠A AD is perpendicular to BC
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
Aa2+b2+c2=4b2Ba2+b2−c2=4b2Ca2−b2+c2=4b2Da2−b2−c2=4b2 - Question 2 - Select One
If D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
Ab2=a2−c2Ba2+b2=5c2C3b2=a2−c2D3a2=b2−3c2 - Question 3 - Select One
In the adjoning figure of ΔABC,AD is the perpendicular bisector of side BC. The triangle ABC is :
 Aright angledBisoscelesCscaleneDequilateral
Aright angledBisoscelesCscaleneDequilateral
In the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :
 View Solution
View SolutionIn the adjoining figure, ABC is a triangle in which AD is the bisector of ∠A. If AD⊥BC, show that △ABC is isosceles.
 View Solution
View SolutionIn a triangle ABC, D is mid-point of BC; AD is produced upto E so that DE = AD Prove that: (i) △ABDand△ECDare congruent. (ii) AB = EC. (ii) AB is parallel to EC
View SolutionIf D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
View SolutionIn a ΔABC, if D is the mid point of BC and AD is perpendicular to AC, then cosB=
View Solution

