In isosceles triangle ABC, ∠B=∠C such that D lies on BC and AD⊥BC then △ABD≅△ACD can be proved by which congruence rule?
SAS
RHS
Both A and B
None of these
The correct Answer is:B
Similar Questions
ఒక సమద్విబహు త్రిభుజము ABC లో AB=AC అయిన ∠B=∠C అని నిరూపించండి.
03:34View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
06:08View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
05:57View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
06:03View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
06:37View SolutionABC is an isosceles triangle with AB=AC and D is a point on ABC BC such that AD⊥BC (see figure ). To prove that ∠BAD=∠CAD a student proceeded as follows
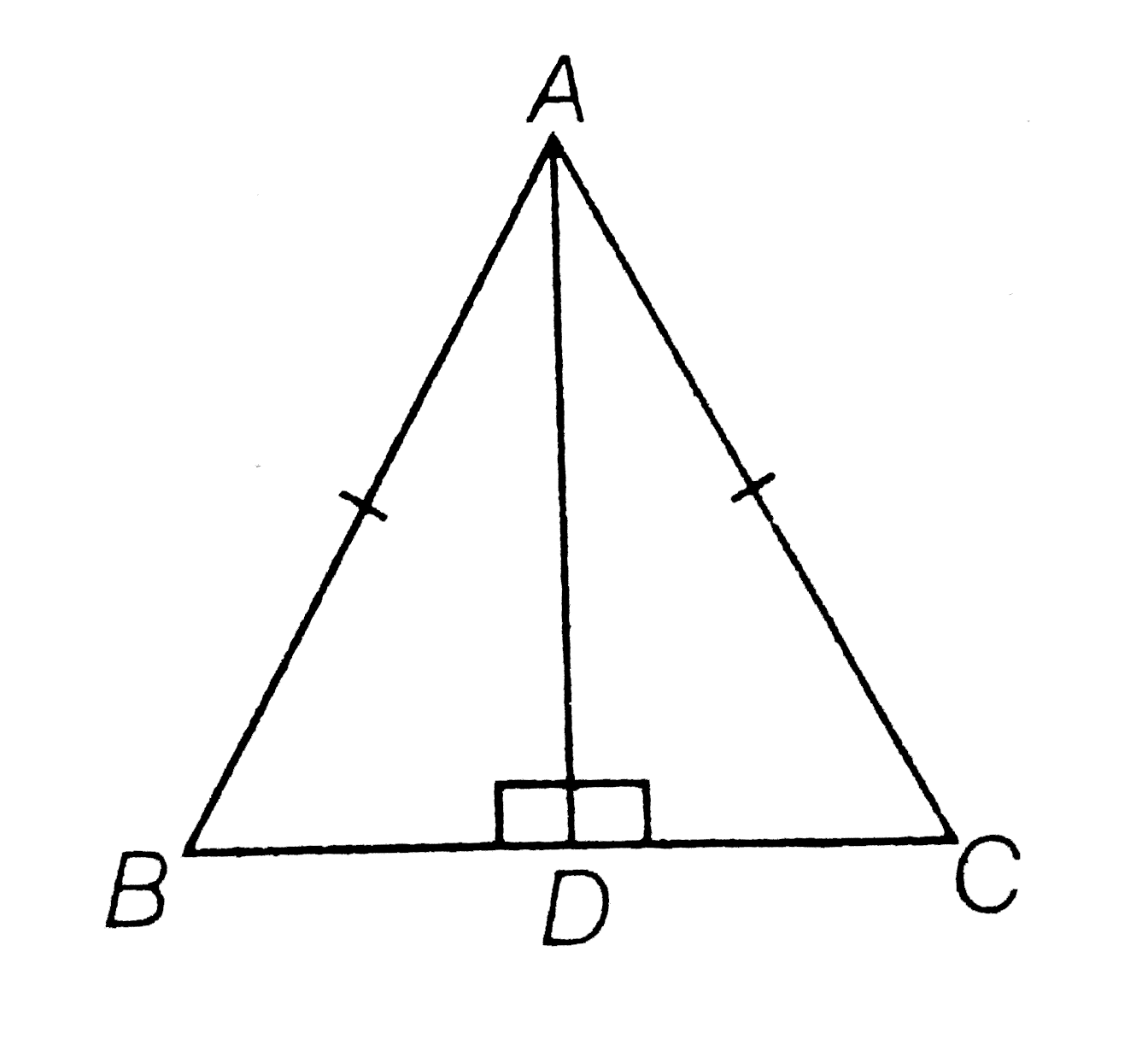
InΔABDandΔACD,we have
AB=AC [ Given]
∠B=∠C [∵ AB=AC ]
and ∠ADB=∠ADC
Therefore ΔABD≅ΔACD [by AAS congruence rule]
So , ∠BAD=∠CAD [byCPCT]
What is the defect in the above argument ?01:58View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
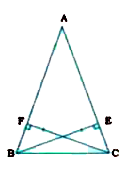 03:33View Solution
03:33View SolutionDelta ABC in, AD Line segment BC The perpendicular of is bisector. Prove that angle ABD = angle ACD
06:22View Solution

