A person is in a room whose ceiling and two adjacent walls are mirrors. How many images are formed
5
6
7
8
The correct Answer is:C
To determine how many images are formed when a person is in a room with mirrors on the ceiling and two adjacent walls, we can follow these steps:
1. Identify the Mirrors:
- We have three mirrors in total:
- Mirror M1 (the ceiling)
- Mirror M2 (one wall)
- Mirror M3 (the adjacent wall)
2. Understand the Geometry:
- The two adjacent walls (M2 and M3) form a 90-degree angle with each other.
3. Calculate Images from Adjacent Walls:
- The formula for the number of images formed by two mirrors at an angle θ is given by:
N=360θ−1
- For our case, θ = 90 degrees:
N=36090−1=4−1=3
- Thus, the two adjacent walls (M2 and M3) will produce 3 images.
4. Calculate Images from the Ceiling:
- The ceiling (M1) will reflect all the images formed by the walls. Since there are 3 images from the walls, each of these images will act as an object for the ceiling mirror.
- The ceiling will also create images of these 3 images. Each of these images will produce 2 additional images (one above and one below), leading to:
Total images from ceiling=3 (images from walls)×2=6
5. Total Images Calculation:
- Now, we sum the images from the walls and the ceiling:
Total Images=Images from walls+Images from ceiling+Original object
- Therefore:
Total Images=3+6+1=10
Final Answer:
The total number of images formed is 10.
---
- We have three mirrors in total:
- Mirror M1 (the ceiling)
- Mirror M2 (one wall)
- Mirror M3 (the adjacent wall)
- The two adjacent walls (M2 and M3) form a 90-degree angle with each other.
- The formula for the number of images formed by two mirrors at an angle θ is given by:
N=360θ−1
- For our case, θ = 90 degrees:
N=36090−1=4−1=3
- Thus, the two adjacent walls (M2 and M3) will produce 3 images.
- The ceiling (M1) will reflect all the images formed by the walls. Since there are 3 images from the walls, each of these images will act as an object for the ceiling mirror.
- The ceiling will also create images of these 3 images. Each of these images will produce 2 additional images (one above and one below), leading to:
Total images from ceiling=3 (images from walls)×2=6
- Now, we sum the images from the walls and the ceiling:
Total Images=Images from walls+Images from ceiling+Original object
- Therefore:
Total Images=3+6+1=10
The total number of images formed is 10.
Topper's Solved these Questions
- RAY OPTICSBOOK - ERRORLESS CHAPTER - RAY OPTICSEXERCISE - Refraction of Light at Plane Surfaces
9 Videos
- RAY OPTICSBOOK - ERRORLESS CHAPTER - RAY OPTICSEXERCISE - Refraction at Curved Surface
8 Videos
- MAGNETISMBOOK - ERRORLESS CHAPTER - MAGNETISMEXERCISE - Assertion & Reason
1 Videos
- WAVE OPTICSBOOK - ERRORLESS CHAPTER - WAVE OPTICSEXERCISE - SET
23 Videos
Similar Questions
Knowledge Check
A person sees his image in a room in which the ceiling and two adjacent walls are mirrors. How. many images are formed?
A5B6C7D8An object is placed between two parallel mirrors. The number of images formed is
A4B6C8DinfinityA man stands symmetrically between two large plane mirrors fixed to two adjacent walls of a reactangular room. The number of images formed as
A4B3C2D6
A plane mirror forms _____ image.
View SolutionA plane mirror forms _____ image.
View SolutionThree plane mirrors are mounted on three walls forming an isosceles right triangle as shown in the figure. How many images are formed in all? Draw a diagram and indicate the positions of the images.
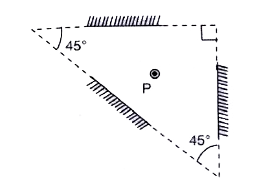
View SolutionA man stands symmetrically between two large plane mirrors fixed to two adjacent walls of a rectangular room. The number of images formed as
View SolutionA cubicla room is formed with 6 plane mirrors. An insect moves along the diagonal of the floor with uniform speed. The speed of its image in two adjacent walls is 20√2cm/s.
Then the speed of the image formed on the roof is
View Solution
