Following figures shows sources S1 and S2 that emits light of wavelength λ in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5λ. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along

Path 1
Path 2
Any path
None of these
The correct Answer is:A
Step by step video, text & image solution for Following figures shows sources S_1 and S_2 that emits light of wavelength lambda in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5lambda. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
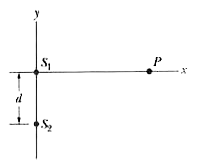
Figure shows two point sources S1 and S2 that emit sound of wavelength λ = 3.00 m. The emissions are isotropic and in phase, and the separation between the sources is d = 16.0 m. At any point P on the x axis, the wave from S1 and the wave from S2 interfere. When P is very far away (x≈0) , what are (a) the phase difference between the arriving waves from S1 and S2 and (b) the type of interference they produce? Now move point P along the x axis toward S1. (c ) Does the phase difference between the waves increase or decrease? At what distance x do the waves have a phase difference of (d) 0.50λ,(e)1.00λ, and (f) 1.50λ?
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O

View Solution
Knowledge Check
Two identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
A(a) Their phase differences remain constantB(b) Their phases are distributed randomlyC(c) Their light intensities remain constantD(d) Their light intensities change randomlyTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .A7λ12B15λ4Cλ2D3λ4
.A7λ12B15λ4Cλ2D3λ4Choose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
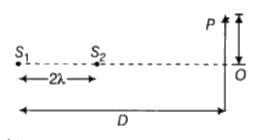 A√2DB√3DC√8DD√5D
A√2DB√3DC√8DD√5D
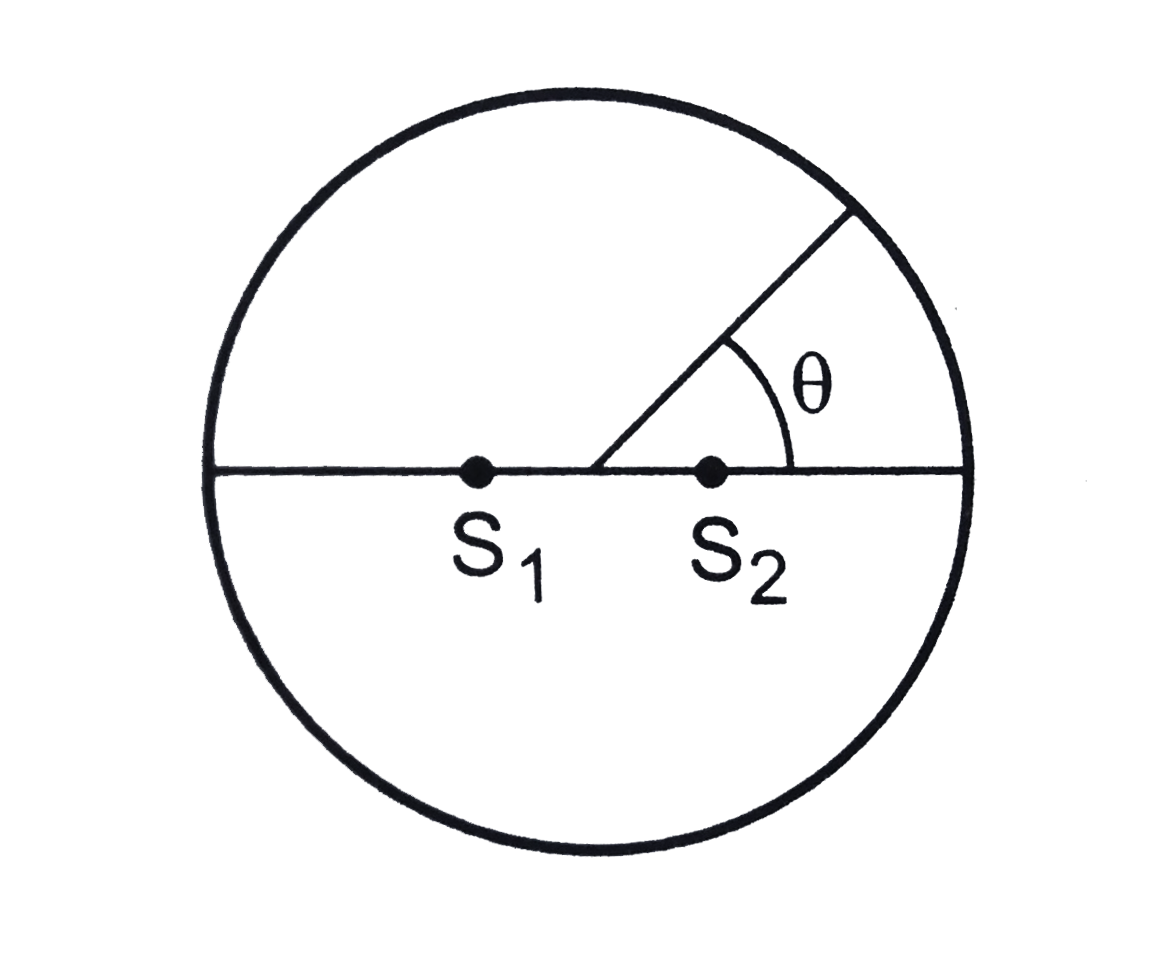
Figure shows two coherent sources S1andS2which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire at large radius is placed in such a way that S1S2 lies in its plane and the middle point of S1S2, is at the centre of the wire. Find the angular positions 0 on the wire for which constructive interference takes place.
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionFigure shows two coherent sources S1 and S2 which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such a way that S1S2 lies in its plane and the middle point of S1S2 is at the centre of the wire. Find the angular positions θ, on the wire for which constructive interference takes place.

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

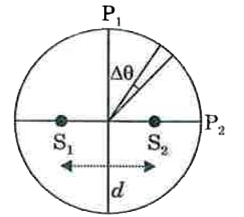
View SolutionTwo coherent monochromatic point sources S1andS2 of wavelength λ=600nm are placed symmetrically on either side of the centre of the circle as shown. The sources are separated by a distance d=1.8mm. This arrangement produces interference fringes visible as alternate bright and dark spots on the circumference of the circle. The angular separation between two consecutive bright spots is Δθ. Which of the following options is/are correct ?
View Solution
