What will be the height of image when an object of 2 mm is placed on the axis of a convex mirror at a distance 20 cm of radius of curvature 40 cm
20 mm
10 mm
6 mm
1 mm
The correct Answer is:d
To find the height of the image formed by a convex mirror when an object of height 2 mm is placed at a distance of 20 cm, we will follow these steps:
1. Identify the Given Data:
- Height of object (ho) = 2 mm
- Object distance (u) = -20 cm (negative because the object is in front of the mirror)
- Radius of curvature (R) = 40 cm
2. Calculate the Focal Length (f):
- The focal length of a convex mirror is given by the formula:
f=R2
- Substituting the value of R:
f=40 cm2=20 cm
- Since it is a convex mirror, the focal length is positive:
f=+20 cm
3. Use the Mirror Formula to Find Image Distance (v):
- The mirror formula is:
1f=1v+1u
- Substituting the known values:
120=1v+1−20
- Rearranging gives:
1v=120+120=220=110
- Therefore, the image distance is:
v=10 cm
4. Calculate the Magnification (m):
- The magnification for mirrors is given by:
m=−vu
- Substituting the values:
m=−10−20=12
5. Calculate the Height of the Image (hi):
- The magnification is also related to the heights of the object and image:
m=hiho
- Rearranging gives:
hi=m⋅ho
- Substituting the values:
hi=12⋅2 mm=1 mm
Final Answer:
The height of the image (hi) is 1 mm.
---
- Height of object (ho) = 2 mm
- Object distance (u) = -20 cm (negative because the object is in front of the mirror)
- Radius of curvature (R) = 40 cm
- The focal length of a convex mirror is given by the formula:
f=R2
- Substituting the value of R:
f=40 cm2=20 cm
- Since it is a convex mirror, the focal length is positive:
f=+20 cm
- The mirror formula is:
1f=1v+1u
- Substituting the known values:
120=1v+1−20
- Rearranging gives:
1v=120+120=220=110
- Therefore, the image distance is:
v=10 cm
- The magnification for mirrors is given by:
m=−vu
- Substituting the values:
m=−10−20=12
- The magnification is also related to the heights of the object and image:
m=hiho
- Rearranging gives:
hi=m⋅ho
- Substituting the values:
hi=12⋅2 mm=1 mm
The height of the image (hi) is 1 mm.
Topper's Solved these Questions
- RAY OPTICSBook:ERRORLESS Chapter:RAY OPTICSExercise:Refraction of Light at Plane Surfaces
Explore 9 Videos
- RAY OPTICSBook:ERRORLESS Chapter:RAY OPTICSExercise:Refraction at Curved Surface
Explore 8 Videos
- MAGNETISMBook:ERRORLESS Chapter:MAGNETISMExercise:Assertion & Reason
Explore 1 Video
- WAVE OPTICSBook:ERRORLESS Chapter:WAVE OPTICSExercise:SET
Explore 23 Videos
Similar Questions
Find the position, magnification and nature of the image of an object placed at a distance of 8 cm from a convex mirror of radius of curvature 24 cm.
View Solution(a) For which position of an object, a concave mirror forms a real image equal in size to the object ?
(b) State one use of a concave mirror.
(c) An object of height 1 cm is placed at a distance of 15 cm from a concave mirror of radius of curvature 20 cm. Find the postition, nature and size of the image formed.
View Solution
Knowledge Check
If an objects is placed 10 cm from a convex mirror of radius of curvature 60 cm, then the position of image is
A7 . 5cmB6 . 5 cmC- 7 . 5 cmD5 . 0 cmWhat acn be the largest distance of an image of a real object from a convex mirror of radius of curvature 20 cm
A10 cmBInfinityC20 cmDNoneA 4.5 cm object is placed perpendicular to the axis of a convex mirror of focal length 15 cm at a distance of 12 cm. The size of the image is
A6.0 cmB4.5 cmC3.0 cmD2.5 cm
An object is placed at a distance of 12cm from a convex mirror of radius of curvature 12 cm. Find the position of the image .
View SolutionAn object is placed at a long distance in front of a convex mirror of radius of curvature 30 cm. State the position of its image.
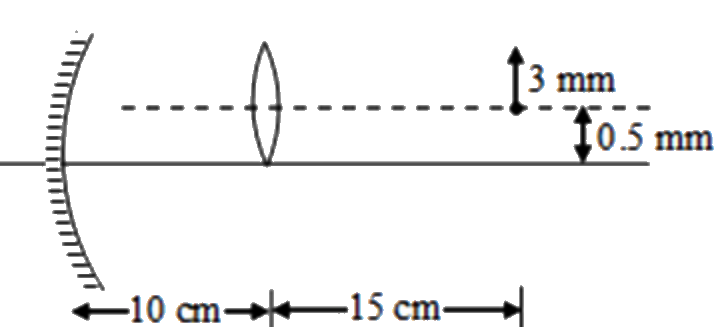
View SolutionA concave mirror of focal length 20 cm and a convex lens of focal length 10 cm are kept with their optic axes parallel but separated by 0.5 mm as shown in the figure. The distance between the the lens and mirror in 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance between the lens and mirror is 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance 15 cm from the lens. Find the length of the image formed the mirror in mm.
View SolutionA 4.5 cm object is placed perpendicular to the axis of a convex mirror of focal length 15 cm at a distance of 12 cm. The size of the image is
View SolutionAn object of height 5 cm is placed in midway between a concave mirror of radius of curvature 30 cm and a convex mirror of radius of curvature 30 cm. The mirrors are placed opposite to each other are and are 60 cm a part, Find the position of the image formed by reflection at convex mirror
View Solution
