If x is the distance of an object from the focus of a concave mirror and y is the distance of image from the focus, then which of the following graphs is correct between x and y
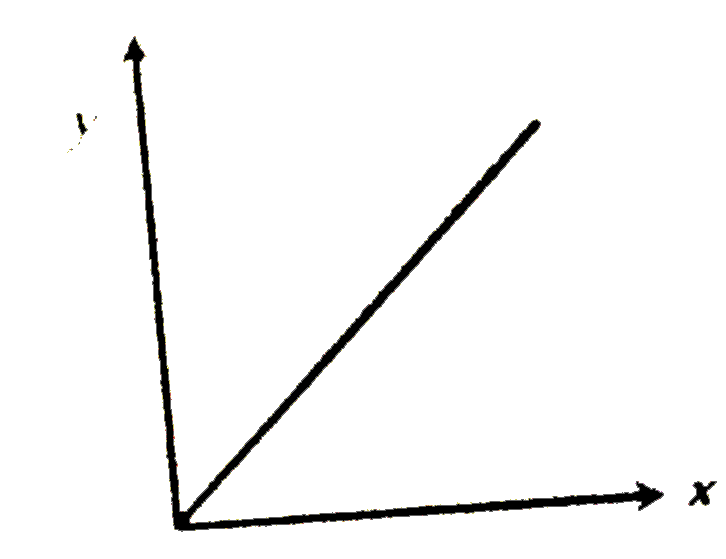
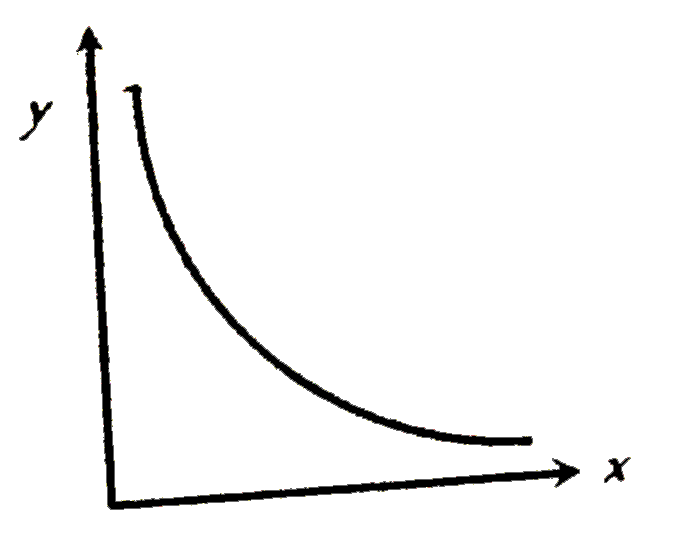
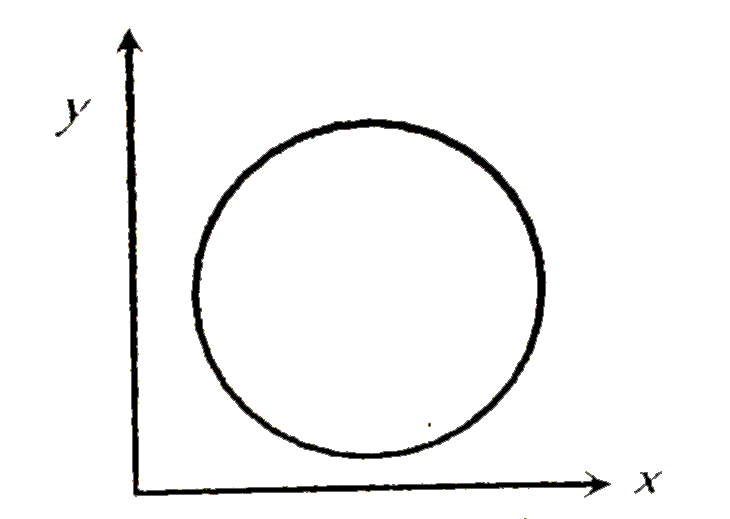
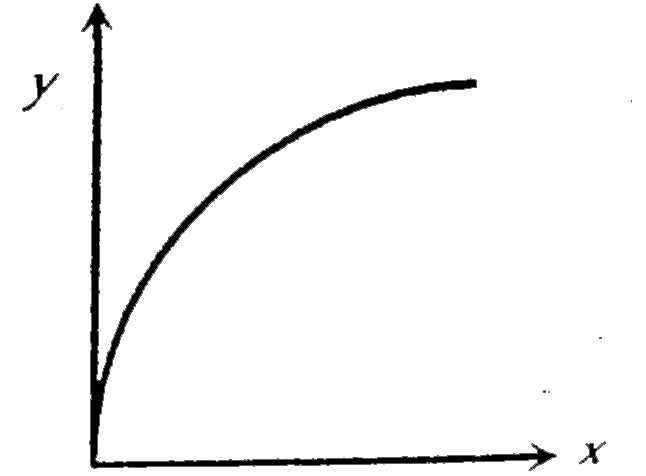
The correct Answer is:b
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - RAY OPTICSEXERCISE - Assertion and Reason4videos
RAY OPTICS
- BOOK - ERRORLESS CHAPTER - RAY OPTICSEXERCISE - SET25videos
RAY OPTICS
- BOOK - ERRORLESS CHAPTER - RAY OPTICSEXERCISE - Critical Thinking4videos
RAY OPTICS
- BOOK - ERRORLESS CHAPTER - MAGNETISMEXERCISE - Assertion & Reason1videos
MAGNETISM
- BOOK - ERRORLESS CHAPTER - WAVE OPTICSEXERCISE - SET23videos
WAVE OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The distance of an object from the fouce of a convex mirror of radius curvature 'a' is 'b' The distance of the image from the focus is:
Ab2/4aBa/b2Ca2/4bD4b/a2 - Question 2 - Select One
An object is placed at the focus of a concave mirror. The
image will beAa real, inverted, same size at the focusBb real, upright, same size at the focusCc virtual, inverted, highly enlarged at infinityDd real, inverted, highly enlarged at infinity - Question 3 - Select One
When the object is at focus of a concave mirror, the image is formed at
AfocusBcentre of curvatureCwithin focusDinfinity
If x and y denote the distance of the object and image from the focus of a concave mirror . The line y=4x cuts the graph at a point whose abscissa is 20 cm. The focal length of the mirror is
_S01_050_Q01.png)
View SolutionWhen an object is held between pole and focus of a concave mirror, the image formed is.
View SolutionWhen an object is placed between the focus and the pole of a concave mirror, the image formed is
View SolutionIf x and y denote the distance of the object and image from the focus of a concave mirror . The line y=4x cuts the graph at a point whose abscissa is 20 cm. The focal length of the mirror is
View SolutionA point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View Solution