Two identical charged spheres suspended from a common point by two masses strings of length l are initially at a distance d (d lt lt 1) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result the charge approaches each other with a velocity v. Then as a function of distance x between them
v∝x−1
v∝x1/2
v∝x
v∝x−1/2
The correct Answer is:D
The repulsive force between the charged spheres,
F=Tsinθ
Weight of each sphere = mg=Tcosθ
∴Tanθ=Fmgorx2l=14πε0q2x2mgorx32l=14πε0⋅q2mg
orq∝3/2
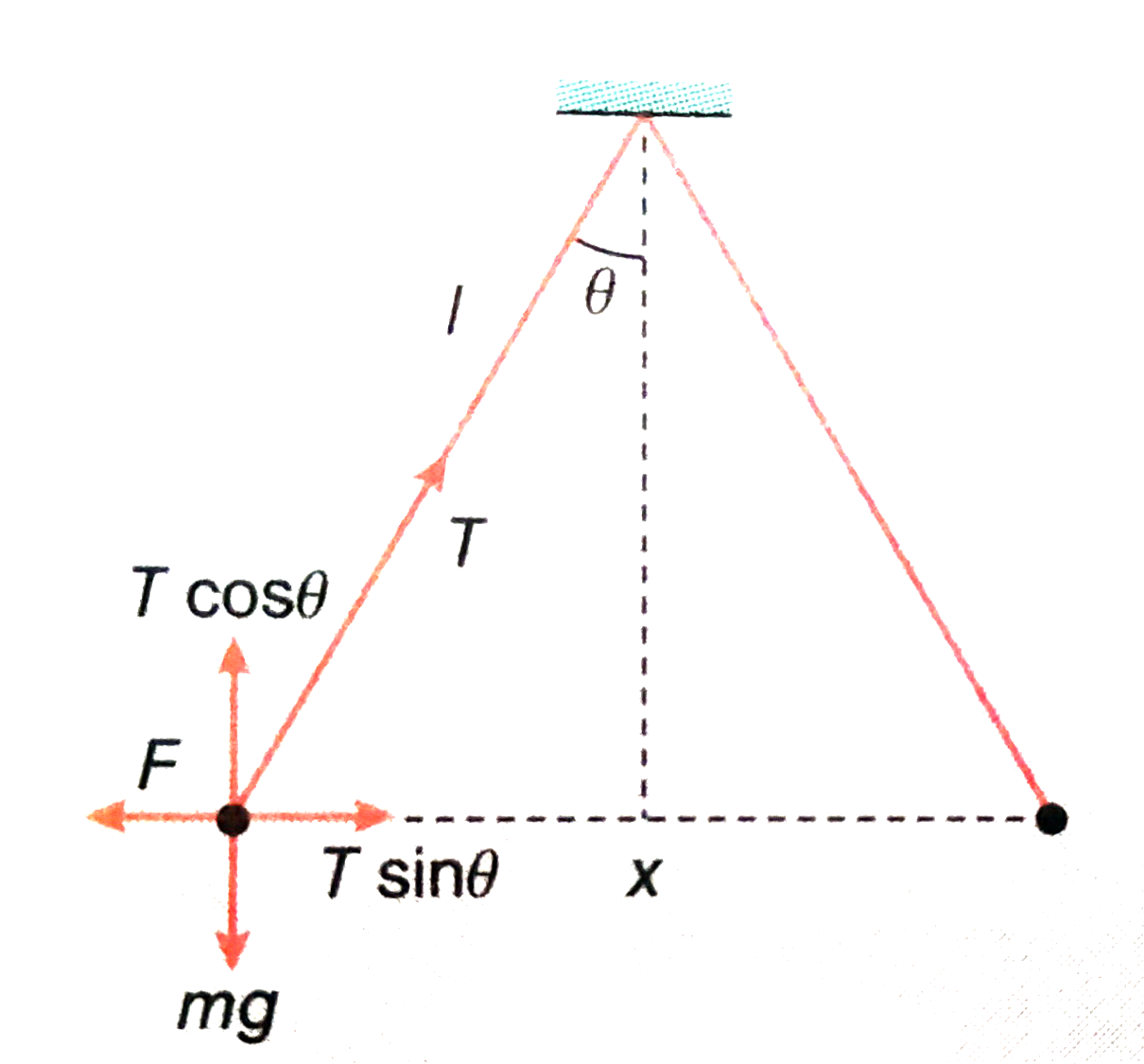
Difference with respect to t,
dqdt∝32x12dxdtor,v∝x−12[∵dqdt = constant].
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - CBSE SCANNER31videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( AIPMT)1videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER7videos
ELECTRIC ENERGY AND POWER
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner13videos
ELECTRIC POTENTIAL
Similar Questions
Two identical charged spheres suspended from a common point by two mass-less strings of length l are initially at a distance d ( d<<l) apart because of their mutual repulsion . The charge begins to leak from both the spheres at a constant rate. As a result the charge approach each other with a velocity v. Then as a function of distance x between them .
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View Solution
Knowledge Check
- Question 1 - Select One
Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d ( d ltlt l) apart because of their mutual repulsion . The charge begins to leak from both the spheres at a constant rate As a result the charge approach each other with a velocity v. Then as a function of distance x between them .
Av∝x1/2Bv∝xCv∝x1/2Dc∝x−1 - Question 2 - Select One
Two identical charged spheres suspended from a common point by two mass-less strings of length l are initially at a distance d ( d<<l) apart because of their mutual repulsion . The charge begins to leak from both the spheres at a constant rate. As a result the charge approach each other with a velocity v. Then as a function of distance x between them .
A(a) v∝x−1B(b) v∝x12C(c) v∝xD(d) v∝x−12 - Question 3 - Select One
Two identical charged spheres suspended from a common point by two mass-less strings of length l are initially at a distance d ( d<<l) apart because of their mutual repulsion . The charge begins to leak from both the spheres at a constant rate. As a result the charge approach each other with a velocity v. Then as a function of distance x between them .
Av∝x12Bv∝xCv∝x12Dv∝x−1
Two indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionTwo identical charged spheres suspended form a common point by two massless strings of lengths l, are initially at a distance d(d>>l) apart because of their mutual repulsion. The charges brgin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity v. Then v varies as a function of the distance x between the spheres, as
View SolutionTwo identical charged spheres suspended from a common point by two mass-less strings of length l are initially at a distance d ( d<<l) apart because of their mutual repulsion . The charge begins to leak from both the spheres at a constant rate. As a result the charge approach each other with a velocity v. Then as a function of distance x between them .
View Solution

