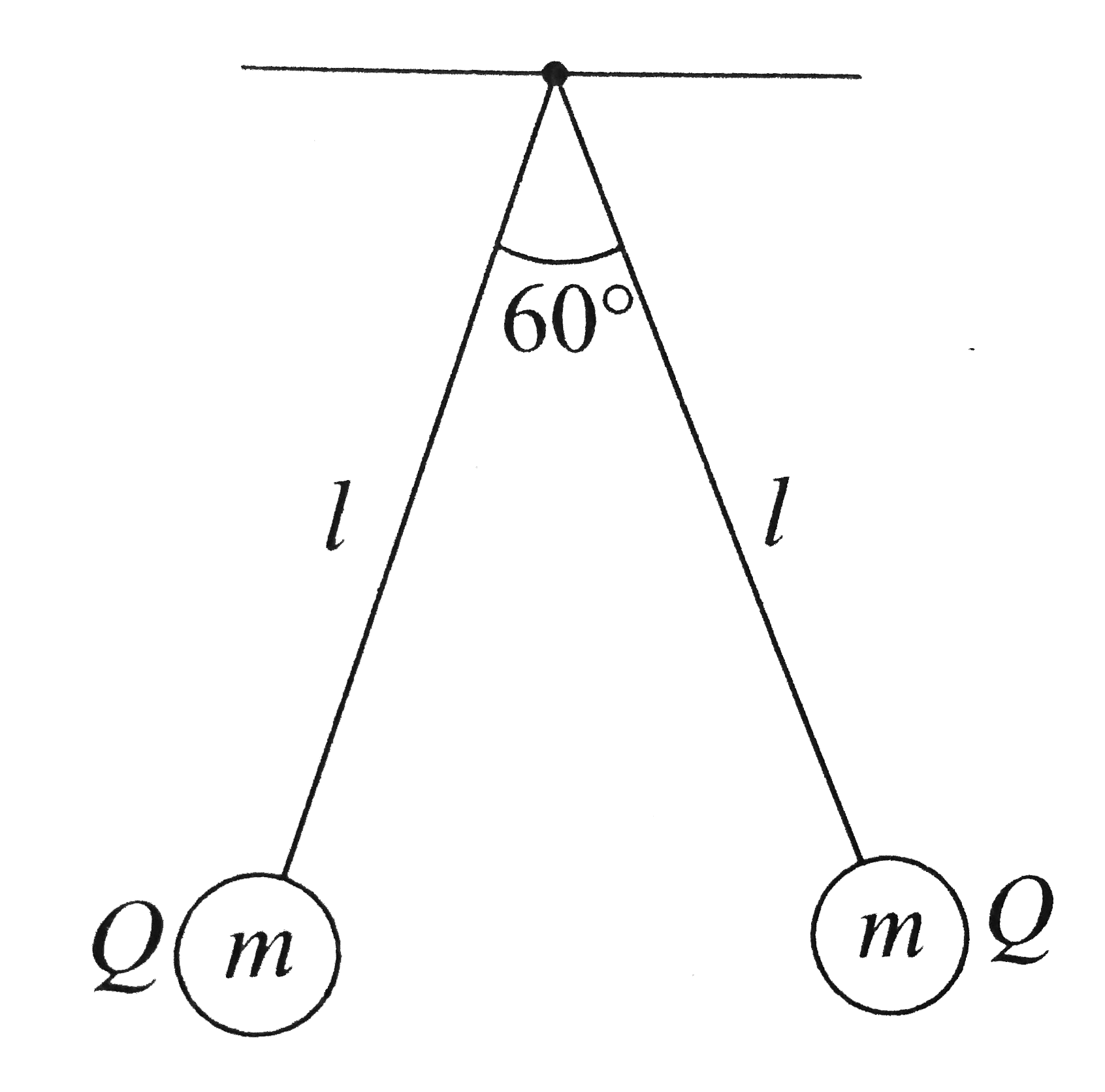
Two identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle $θ$ with the vertical when the spheres are in equilibrium . Calculate the value of q.

Text Solution

Verified by Experts

The force acting on the charged particles suspended from the strings is shown in the figure. There will be tension in the wire due to the force of repulsion between the two charges.

At equilibrium , for charge at A, vertical component of tension in the string will be balanced by the weight of the charge .
$T \cos θ = m g$ …(i)
Where, $\cos θ = \frac{x}{l}$
Also, $T \sin θ = F_{E} = \frac{1}{4 π ε_{0}} \frac{q . q}{{(2 x)}^{2}}$ , where $F_{E}$ is the force of repulsion between charges at A and B .
$\Rightarrow T \sin θ = F_{E} = \frac{1}{4 π ε_{0}} \frac{q^{2}}{{(2 l \cos θ)}^{2}}$ …(ii) ( $∵ x = l \cos θ$ )
On dividing equation (i) by (ii) , we get
$\frac{\sin θ}{\cos θ} = \frac{1}{4 π ε_{0}} \times \frac{q^{2}}{4 l^{2} \cos^{2} θ} \times \frac{1}{m g}$
$\Rightarrow q^{2} = 16 π ε_{0} m g l^{2} \sin^{2} θ \times \tan θ$
$q = 4 l \sin θ \sqrt{π ε_{0} m g \tan θ}$

Updated on:21/07/2023

Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle $' θ'$ with the vertical ?
A $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 2}$
B $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 3}$
C $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g})}^{1 / 3}$
D $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g^{2}})}^{1 / 3}$
A small sphere of mass $m$ suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of $θ$ measured from the vertical is $g \sqrt{1 + 3 {cos}^{3} θ}$
BThread tension as a function of $θ$ measured from the vertical is $T = 3 m g cos θ$
CThe angle $θ$ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is ${cos}^{- 1} 1 / \sqrt{3}$ .
DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be $m g$ .
Two small balls, each having equal positive charge $Q$ are suspended by two insulationg strings of equal length $l$ from a hook fixed to a stand. It mass of each ball $= m$ and total angle between the two strings is $60^{\circ}$ m, then find the charge on each ball.

A $L \sqrt{\frac{\sqrt{3} m g}{k}}$
B $L \sqrt{\frac{m g}{\sqrt{3} k}}$
C $L \sqrt{\frac{m g}{k}}$
D $\frac{L}{3} \sqrt{\frac{m g}{k}}$