At each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.
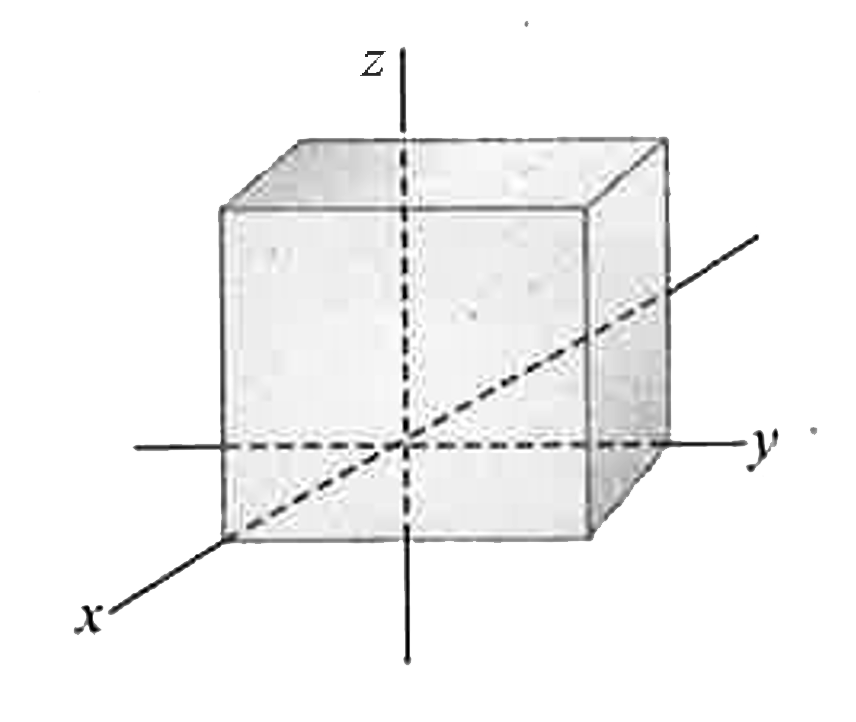
The correct Answer is:−486N.m2/C
Step by step video, text & image solution for At each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is vecE=34hatk N//C and on the bottom face it is vecE=20hatk N//C . Find the net flux contained within the cube. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension
36 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
Similar Questions
The electric field in a cubical volume is
→E=E0(1+za)ˆi+E0(za)ˆj
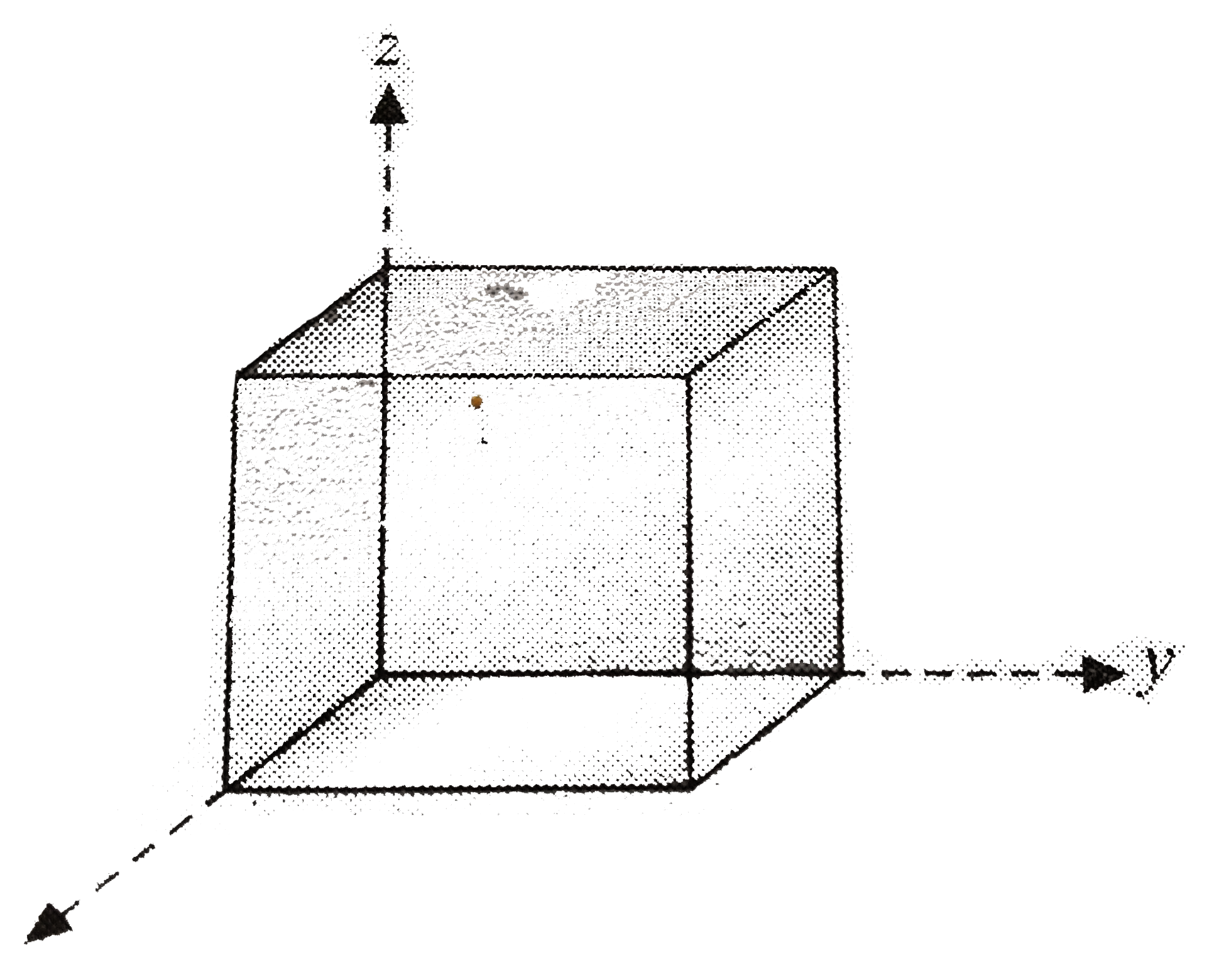
Each edge of the cube measures d, and one of the corners lies at the origin of the coordinates. Determine the net charge within the cube.
View SolutionA point charge q is placed at the centre of a cube. What is the flux linked.
a with all the faces of the cube?
b. with each face of the cube?
c. if charge is not at the centre, then what will be the answer of parts a and b ?
View Solution
Knowledge Check
A charge qμC is placed at the centre of a cube of a side 0.1m, then the electric flux diverging from each face of the cube is
Aq×10−624ε0Bq×10−4ε0Cq×10−66ε0Dq×10−412ε0A charge of q μC is placed at the centre of a cube of side 0.1 m. the electric flux diverging from each face of the cube will be
Aq×10−6ε0 VmBq×10−66ε0 VmC6q×10−6ε0VmDq×10−4(ε0)VmA solid cube of wood of side 2a and mass M is resting on a horizontal surface as shown in the figure. The cube is free to rotate about a fixed axis AB. A bullet of mass m (<<M) and speed v is shot horizontally at the face opposite to ABCD at a height 4a/3 from the surface to impart the cube an angular speed ω. It strike the face and embeds in the cube. Then ωc is close to (note : the moment of inertia of the cube about an axis perpendicular to the face and passing through the center of mass is 2Ma2/3)
 AMv/maBMv/2maCmv/MaDmv/2Ma
AMv/maBMv/2maCmv/MaDmv/2Ma
Twelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

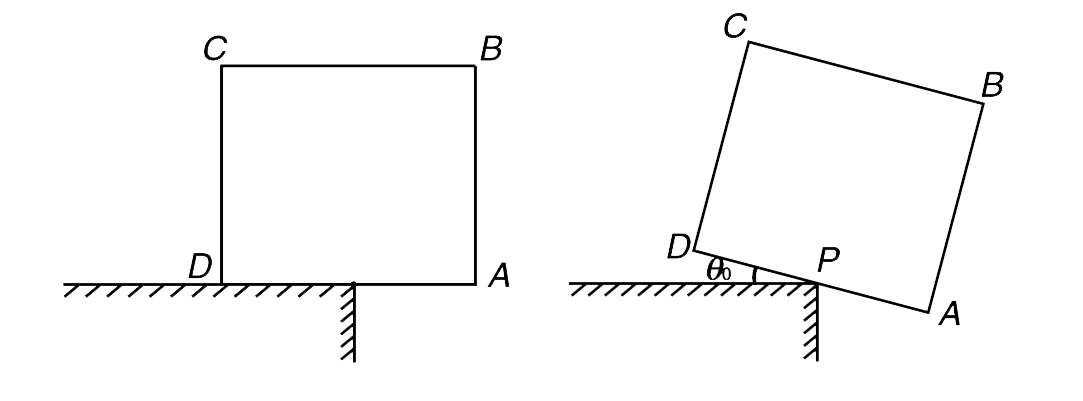
View SolutionA uniform cube of mass M and side length a is placed at rest at the edge of a table. With half of the cube overhanging from the table, the cube begins to roll off the edge. There is sufficient friction at the edge so that the cube does not slip at the edge of the table. Find -
(a) the angle θ0 through which the cube rotates before it leaves contact with the table.
(b) the speed of the centre of the cube at the instant it breaks off the table.
(c) the rotational kinetic energy of the cube at the instant its face AB becomes horizontal.
View SolutionA cube of side 20 cm is kept in a region as shown in the figure. An electric field →E exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m.
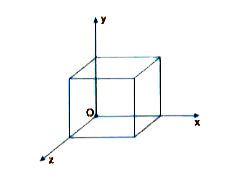
Find the
(i) electric field →E, and
(ii) total electric flux through the cube.
View SolutionIn a uniform electric field, a cube of side 1 cm is placed. The total energy stored in the cube is 8.85μJ. The electric field is parallel to four of the faces of the cube. If the electric flux through any one of the remaining two faces is m√n volt-meter, then find (mn).
View SolutionA solid cube of wood of side 2a and mass M is resting on a horizontal surface as shown in the figure. The cube is free to rotate about the fixed axis AB. A bullet of mass m (<<M) and speed v is shot horizontally at the face opposite to ABCD at a height 'h' above the surface to impart the cube an angular speed ωc so that the cube just topples over. Then ωc is (note : the moment of inertia of the cube about an axis perpendicular to the face and passing through the center of mass is 2Ma3/3)
View Solution
