A cube of side 20 cm is kept in a region as shown in the figure. An electric field →E exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m.
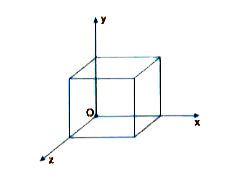
Find the
(i) electric field →E, and
(ii) total electric flux through the cube.
Text Solution
(i) Here potential V=10x+5
∴ Electric field →E=−dVdr=−∂V∂xˆi−∂V∂yˆj−∂V∂zˆk=−10ˆiVm−1
(ii) As →E is directed along x-axis and is constant at all points, so we shall have flux associated with two opposite faces of cube in y-z plane. However, flux with each of the two faces is equal but at one face it is outgoing and at the other it is incoming one. Hence, net flux ϕB=0.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 EXERCISE - SECTION C10videos
CBSE EXAMINATION PAPER 2020
- BOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - SELF ASSESSMENT TEST (SECTION C)2videos
ATOMS
- BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D11videos
CBSE EXAMINATION PAPER 2020 (SOLVED)
Similar Questions
Knowledge Check
- Question 1 - Select One
Let V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
AV0−4x−5yBV0+4x+5yC4x+5y−V0D−4x−5y - Question 2 - Select One
A cube of edge a is kept on x-axis in a region where electric field varies with distance as E=kxˆi. Total electric flux associated with the cube is-
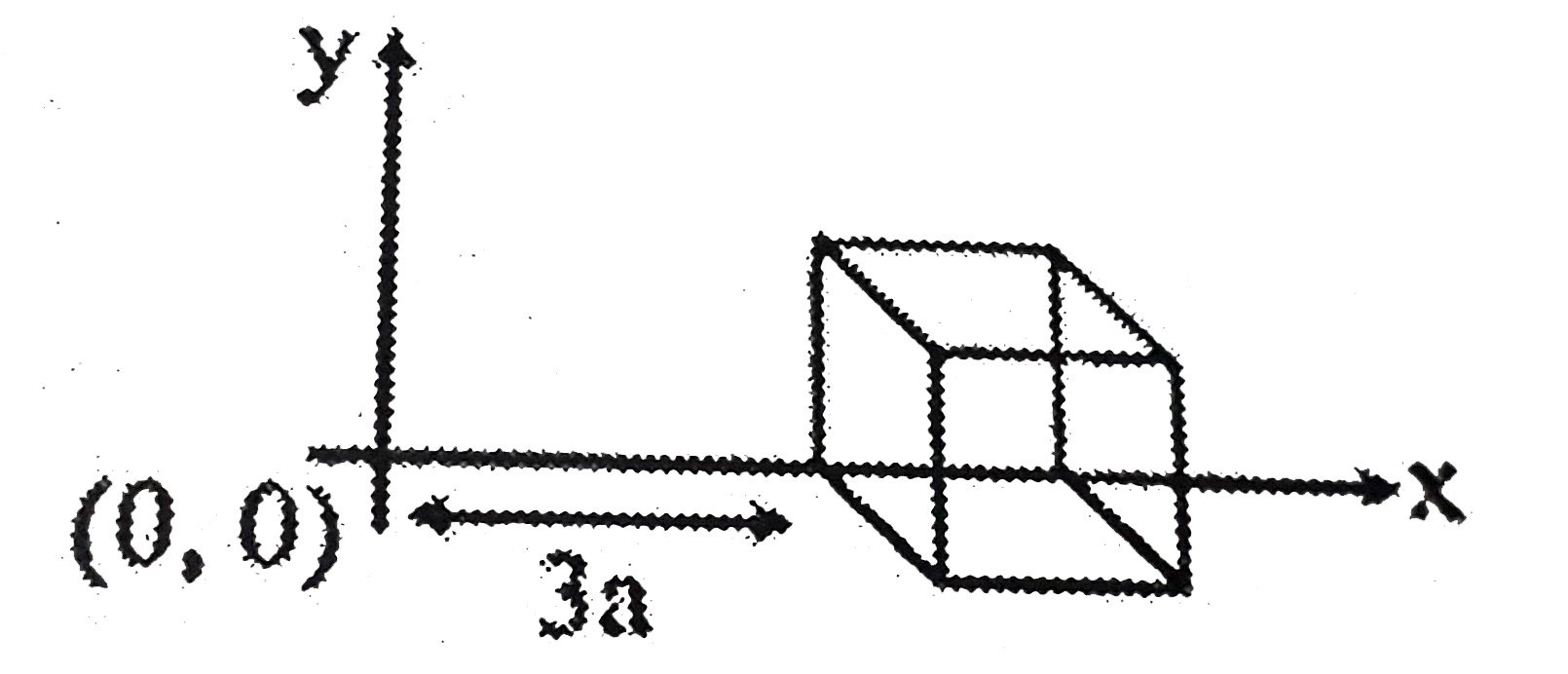 Aka3B−3ka3C4ka3Dzero
Aka3B−3ka3C4ka3Dzero - Question 3 - Select One
Find the electric field in region II as shown in figure.
 AzeroBσ4πε0Cσε0DInfinite
AzeroBσ4πε0Cσε0DInfinite
Given the electric field in the region →E=2ξ, find the net electric flux through the cube and enclosed by it.
 View Solution
View SolutionFind the electric field in region II as in figure shown.
 View Solution
View SolutionDeduce the expression for electric potential in a region of electric field →E=Kx2ˆi. Consider that electric potential at infinity is zero.
View SolutionThe electirc potential at a point (x,y,z) is given by
V=−x2y−xz3+4
The electric field →E at that point isView SolutionThe electirc potential at a point (x,y,z) is given by
V=−x2y−xz3+4
The electric field →E at that point isView Solution

