An infinite ladder network is constructed with 1Ωand 2Ω resistors as shown. Find the equivalent resistance points A and B. 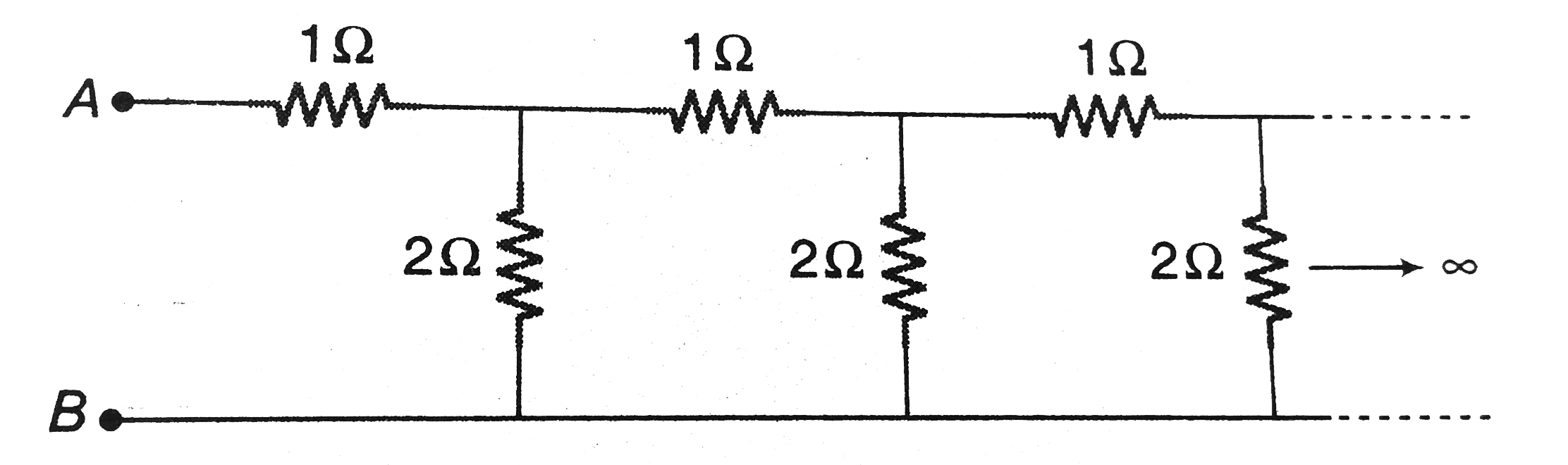
Let the equivalent resistance between A and B is x. We may consider the given circuit as shown in figure.
in this diagram 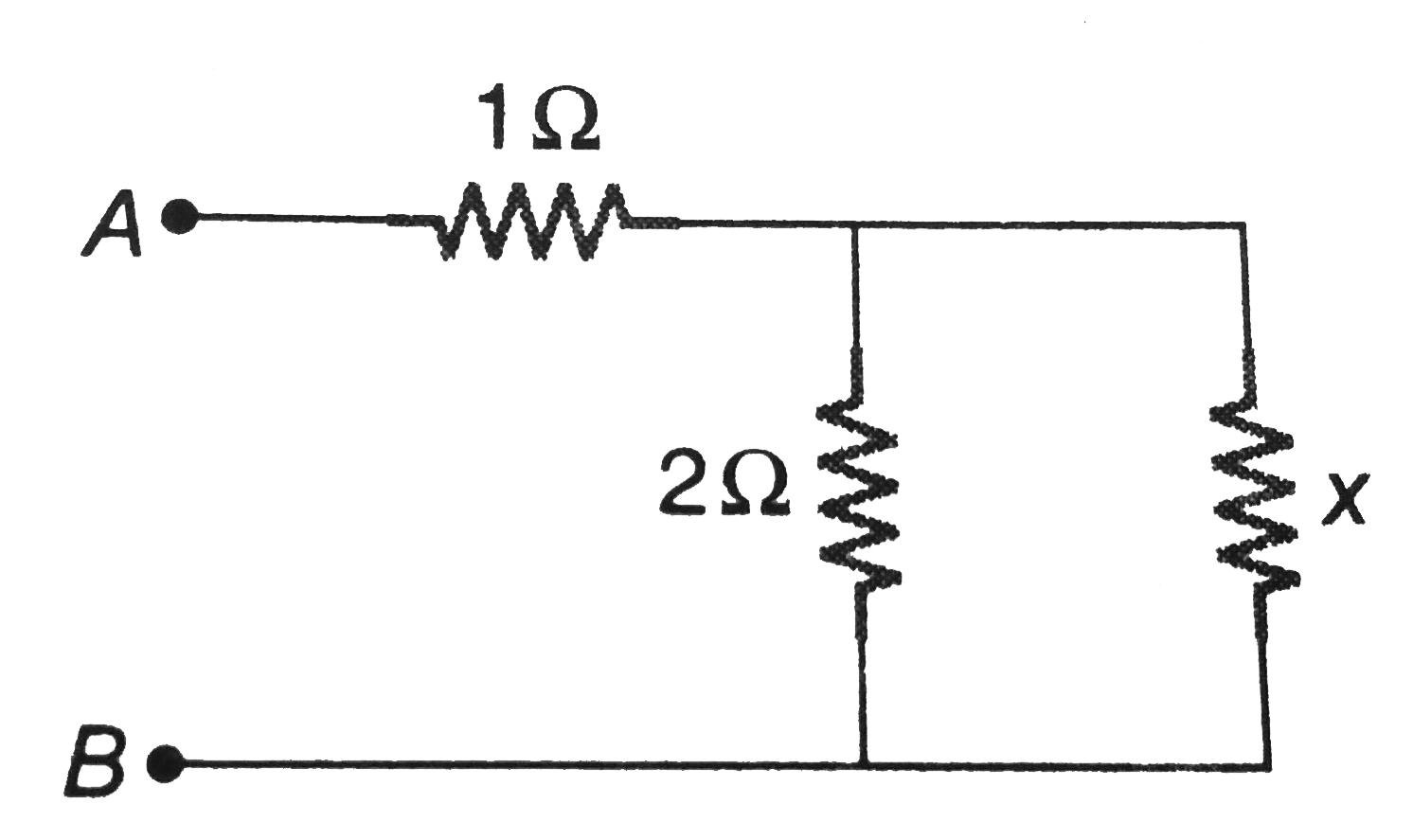
RAB=2x2+x+1 or x+2x2+x+1 (as RAB=x)
or x(2+x)=2x+2+x or x2−x−x−2=0
x=1±√1+82=−1Ω and 2Ω
Ignoring the negative value, we have RAB=x=2Ω
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
155 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
An infinite ladder network of resistances is constructed with 1Ωand2Ω resistances as shown
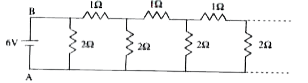
View SolutionAn infinite ladder is constructed with 1(Ω)and 2(Ω)resistor as shown in figure.(a)Find the effective resistance between the point A and B. (b) Find the current that passes through the (2Ω) resistor nearest to the battery.

View SolutionIn the network shown, the equivalent resistance between A and B is

View SolutionFor the combination of resistors shown in Fig. find the equivalent resistance between the points
A and B

View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and B,
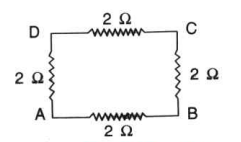
View SolutionFind in the given network of resistors, the equivalent resistance between the points A and B
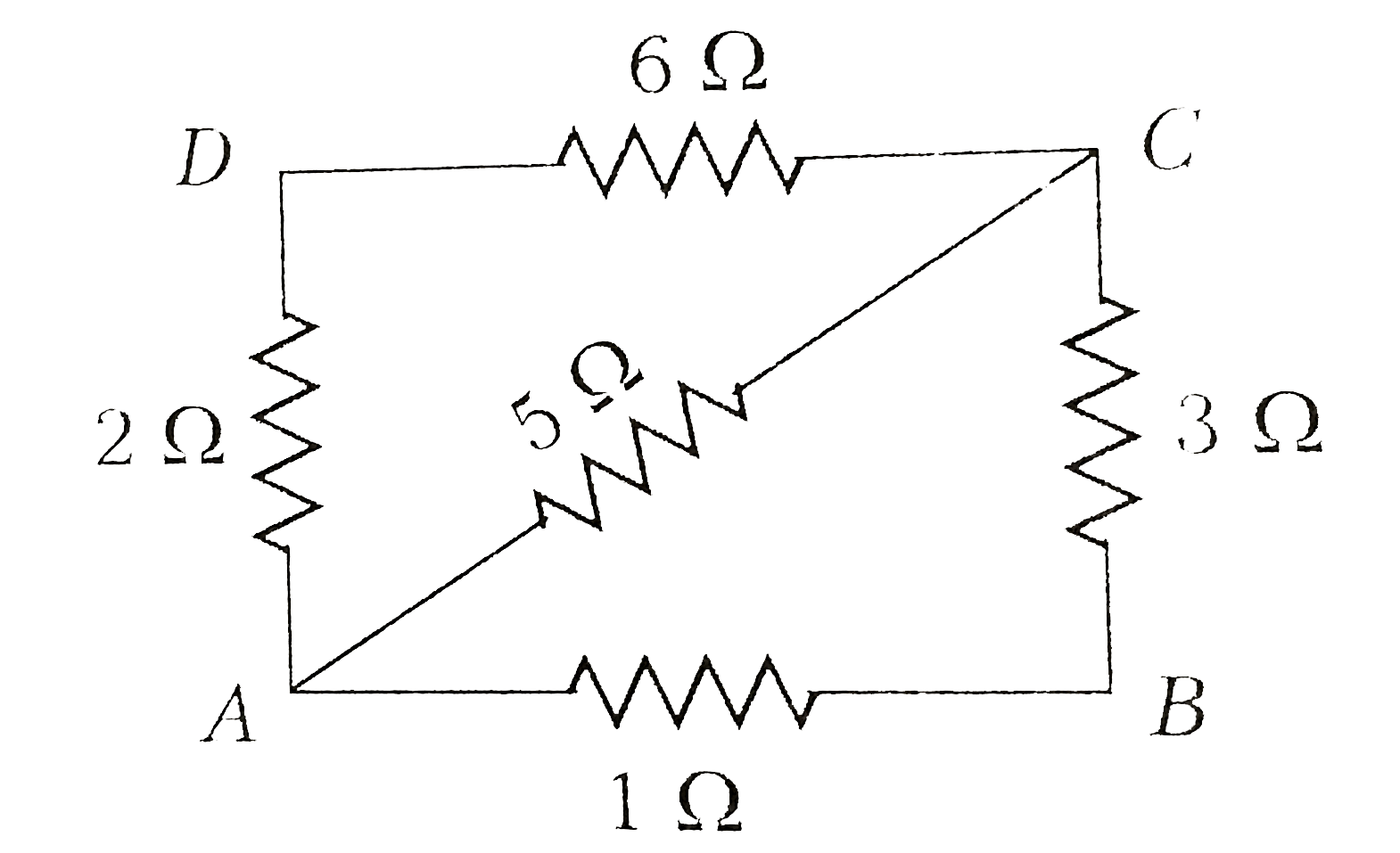
View SolutionIn the network of resistors shown in the adjoining figure, the equivalent resistance between A and B is
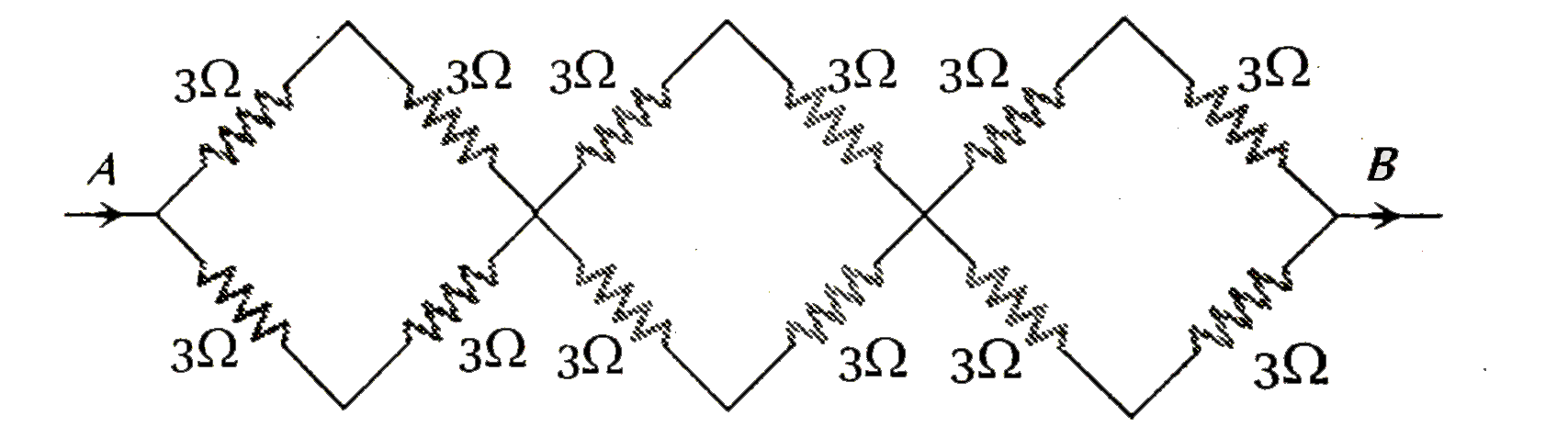
View SolutionEach resistance is of 1Ω in the circuit diagram shown in figure. Find out equivalent resistance between A and B.
View SolutionFind the equivalent resistance of the network shown in figure
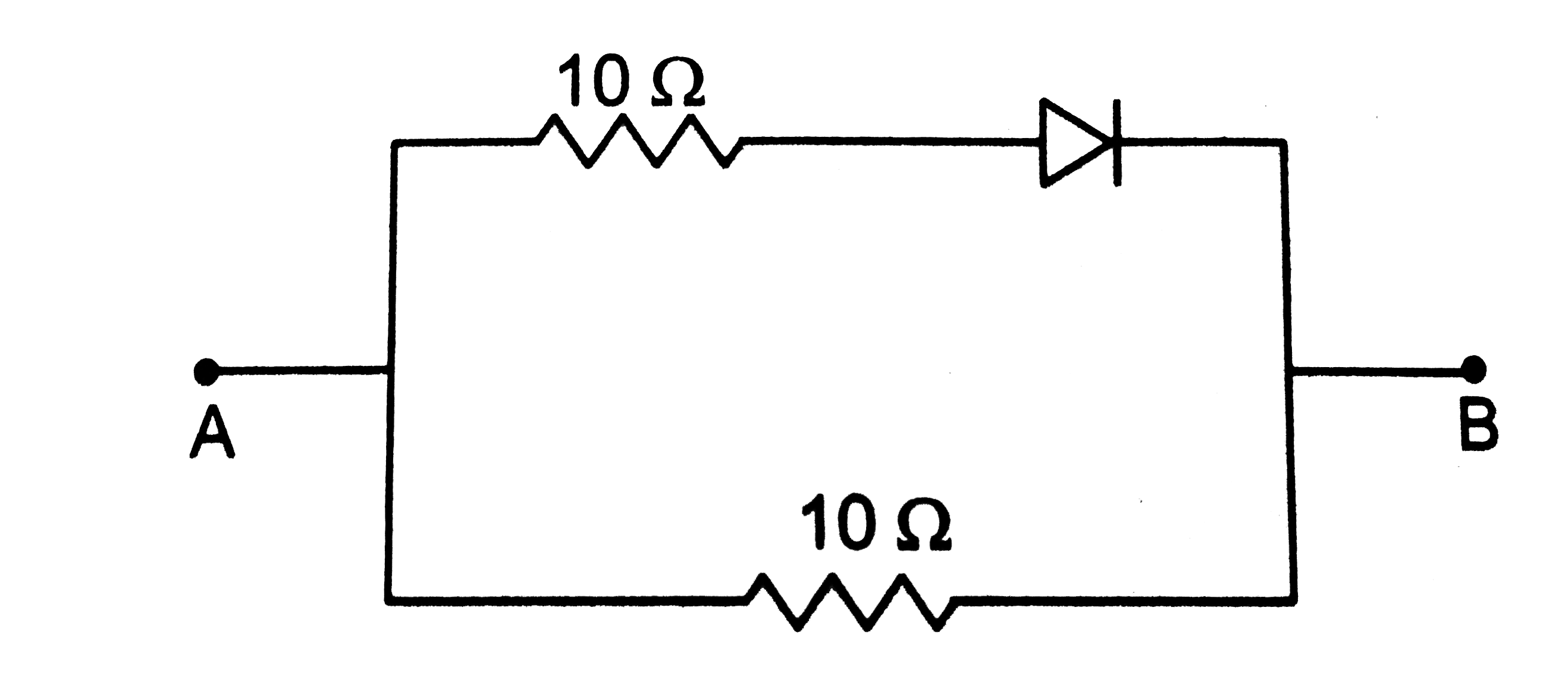
View SolutionFor infinite ladder network containing identical resistance of RΩ each, are combined as shown in figure. The equivalent resistance between A and B is RAB and between A and C is RAC. Then the value RABRAC is :

View Solution
