A very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformly charged line charge( linear charge density λ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
λ=Rσ
λ=−Rσ
λ=2πRσ
λ=−2πRσ
The correct Answer is:d
To solve the problem, we need to analyze the electric fields produced by both the charged cylinder and the charged line along the cylinder's axis. We will use Gauss's law and the principle of superposition.
1. Identify the Electric Field due to the Charged Cylinder:
The electric field Ecylinder outside a uniformly charged cylinder with surface charge density σ can be calculated using Gauss's law. For a cylindrical Gaussian surface of radius r (where r>R), the electric field is given by:
Ecylinder=σRϵ0r
where ϵ0 is the permittivity of free space.
2. Identify the Electric Field due to the Charged Line:
The electric field Eline due to a long line charge with linear charge density λ at a distance r from the line charge is given by:
Eline=λ2πϵ0r
3. Set Up the Condition for Zero Electric Field Outside the Cylinder:
According to the problem, the total electric field outside the cylinder is zero. Therefore, we can write:
Ecylinder−Eline=0
This implies:
Ecylinder=Eline
4. Substitute the Expressions for the Electric Fields:
Substituting the expressions from steps 1 and 2 into the equation gives:
σRϵ0r=λ2πϵ0r
5. Simplify the Equation:
We can cancel ϵ0r from both sides (assuming r≠0):
σR=λ2π
6. Solve for λ:
Rearranging the equation gives:
λ=2πσR
Final Answer:
The value of the linear charge density λ is:
λ=2πσR
The electric field Ecylinder outside a uniformly charged cylinder with surface charge density σ can be calculated using Gauss's law. For a cylindrical Gaussian surface of radius r (where r>R), the electric field is given by:
Ecylinder=σRϵ0r
where ϵ0 is the permittivity of free space.
The electric field Eline due to a long line charge with linear charge density λ at a distance r from the line charge is given by:
Eline=λ2πϵ0r
According to the problem, the total electric field outside the cylinder is zero. Therefore, we can write:
Ecylinder−Eline=0
This implies:
Ecylinder=Eline
Substituting the expressions from steps 1 and 2 into the equation gives:
σRϵ0r=λ2πϵ0r
We can cancel ϵ0r from both sides (assuming r≠0):
σR=λ2π
Rearranging the equation gives:
λ=2πσR
The value of the linear charge density λ is:
λ=2πσR
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type
7 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
Similar Questions
A long charged cylinder of linear charge density λ surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders?
View SolutionA long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cyclinder. What is the electric field in the space between the two cylinders ?
View Solution
Knowledge Check
A very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformly charged line charge( linear charge density λ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
Aλ=RσBλ=−RσCλ=2πRσDλ=−2πRσFind ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
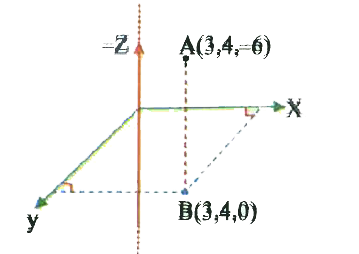 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1If the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
A4×105NC−1B2×106NC−1C8×107NC−1D12×107NC−1
A long charged cylinder of linear charged density à is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View SolutionAn infinitely long time charge has linear charge density λC/m the line charge is along the line x=0,z=2m find the electric field at point (1,1,1) m.
View SolutionFind the electric field at the origin due to the line charge (ABCD) of linear charge density λ,

View SolutionThe electric intensity at a point near a charged conductor of surface charge density σ is
View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View Solution
