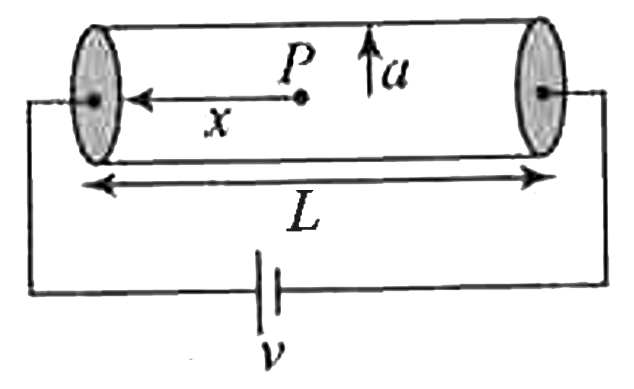
A cylindrical solid of length L and radius a is connected across a source of emf V and negligible internal resistance shown in figure. The resistivity of the rod at point P at a distance x from left end is given by ρ=bx (where b is a positive constant). Find the electric field at point P.
The correct Answer is:B
Step by step video, text & image solution for A cylindrical solid of length L and radius a is connected across a source of emf V and negligible internal resistance shown in figure. The resistivity of the rod at point P at a distance x from left end is given by rho=bx (where b is a positive constant). Find the electric field at point P. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Combination of Resistance 1
14 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Combination of Resistance 2
14 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - QUESTION BANK
40 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
Similar Questions
A cylindrical solid of length 1m and radius 1m is connected across a source of emf 10V and negligible internal resistance shown in the figure. The resistivity of the rod as a function of x(x meastred from left end) is given by p=bx (where b is a positive constant). Find the electric field (in SI unit) at point P at a distance 10cm from left end.
'(##CEN_KSR_PHY_JEE_CO20_E01_030_Q24##)'
View SolutionA 10 V cell of neglible internal resitsance is connected in parallel across a battery of emf 200 V and internal resistance 38Ω as shown in the figure. Find the value of current in the circuit.

View Solution
Knowledge Check
A cell E1 of emf 6V and internal resistance 2Ω is connected with another cell E2 of emf 4V and internal resistance 8Ω (as shown in the figure). The potential difference across points X and Y is :
 A10.0 VB3.6 VC5.6VD2.0 V
A10.0 VB3.6 VC5.6VD2.0 VA conductor of resistivity ρ and resistance R, as shown in the figure, is connected across a battery of emf V. Its radius varies from a at left end to b at right end. The electric field at a point P at distance x from left end of it is
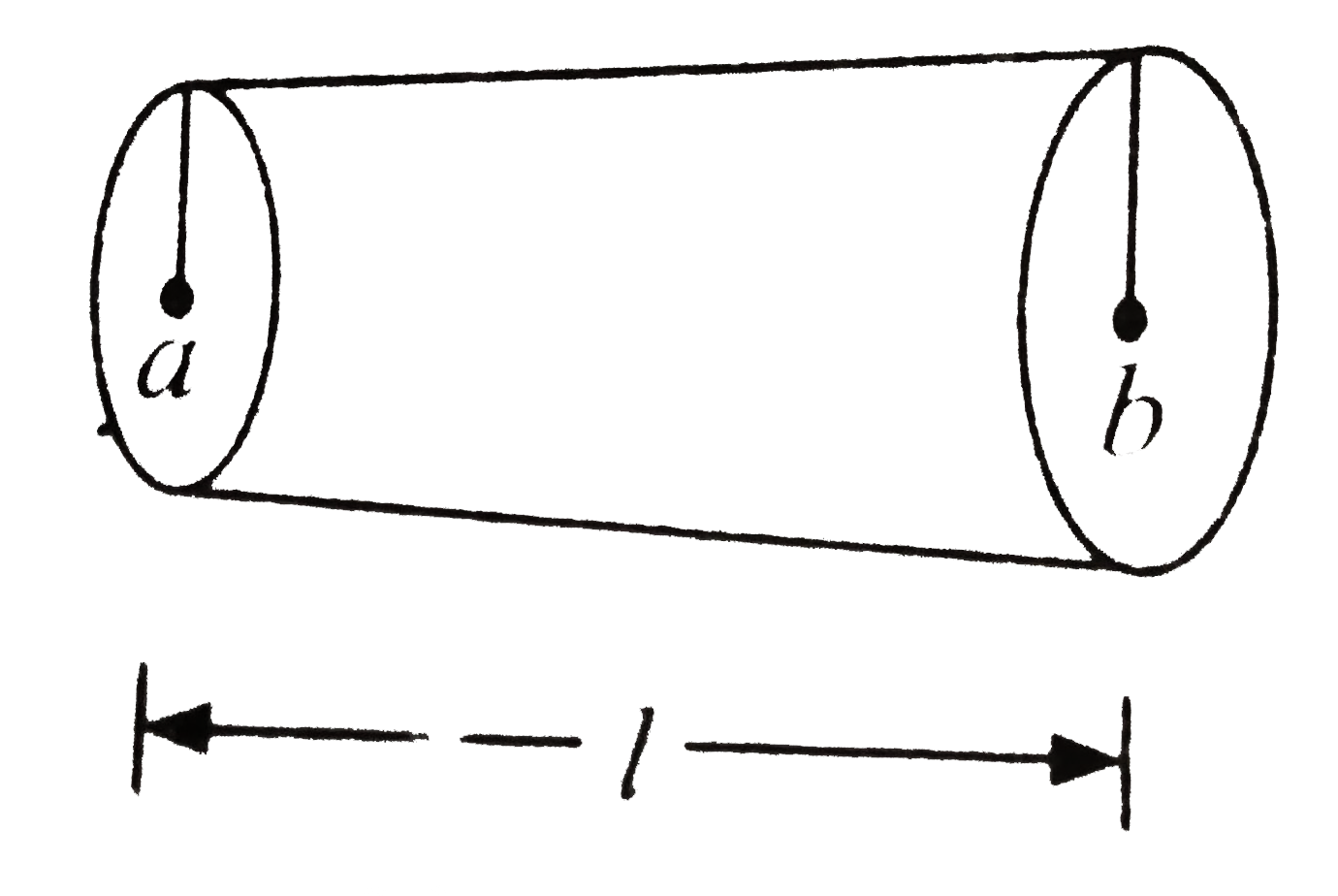 AVI2ρπR[Ia+(b−a)x]2B2VI2ρπR[Ia+(b+a)x]2CVI2ρ2πR(Ia+(b−a)x)2Dnone of these
AVI2ρπR[Ia+(b−a)x]2B2VI2ρπR[Ia+(b+a)x]2CVI2ρ2πR(Ia+(b−a)x)2Dnone of theseA cylindrical conductor AB of length l and area of cross-section a is connected to a battery having emf E and negligible internal resistance. The specific conductivity of cylindrical conductor varies as σ=σ01√x, where σ0 is constant and x is distance from end A. What is the electric field just near the end B of cylinder?
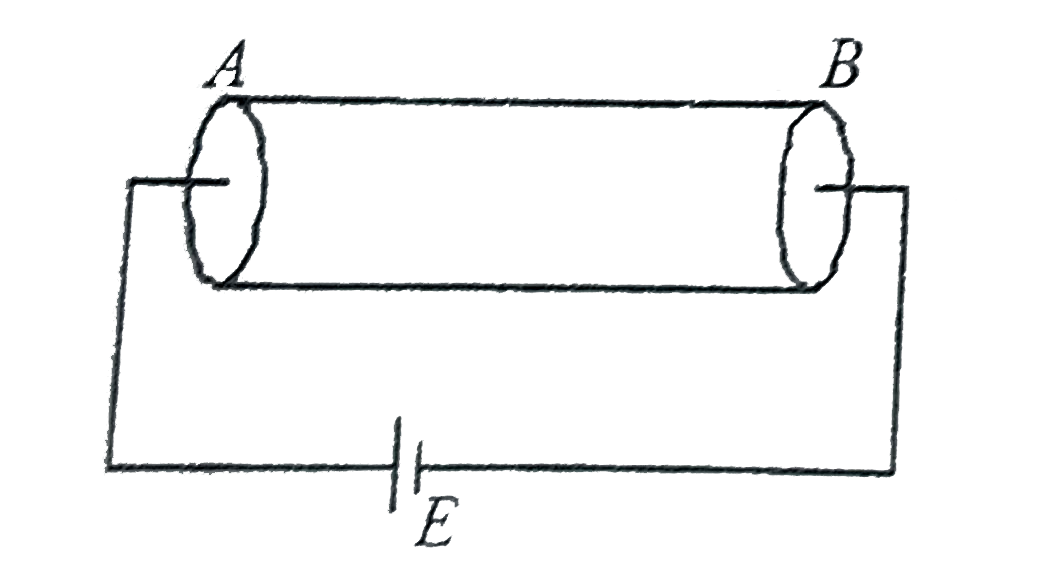 AElB3E2lC2E3lDE2l
AElB3E2lC2E3lDE2l
Find the current drawn from a cell of emf 1 V and internal resistance (2/3)Ω connected to the network shown in figure

View SolutionA long cylindrical conductor of cross-sectional area A and radius a is made of material whose resistivity depends only on a distance r from the axis of conductor, given by ρ=cr2, where c is a constant. Find the resistance per unit length of the conductor and the electric field strength due to which a current I flows in it.
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA 10 V cell of negligible internal resistance is connected in parallel across a battery of emf 200 V and internal resistance 38 Ω as shown in the Fig. Find the value of current in the circuit.

View SolutionA battery of e.m.f. 10V is connected to resistance as shown in figure. The potential difference VA−VB between the point A and B is
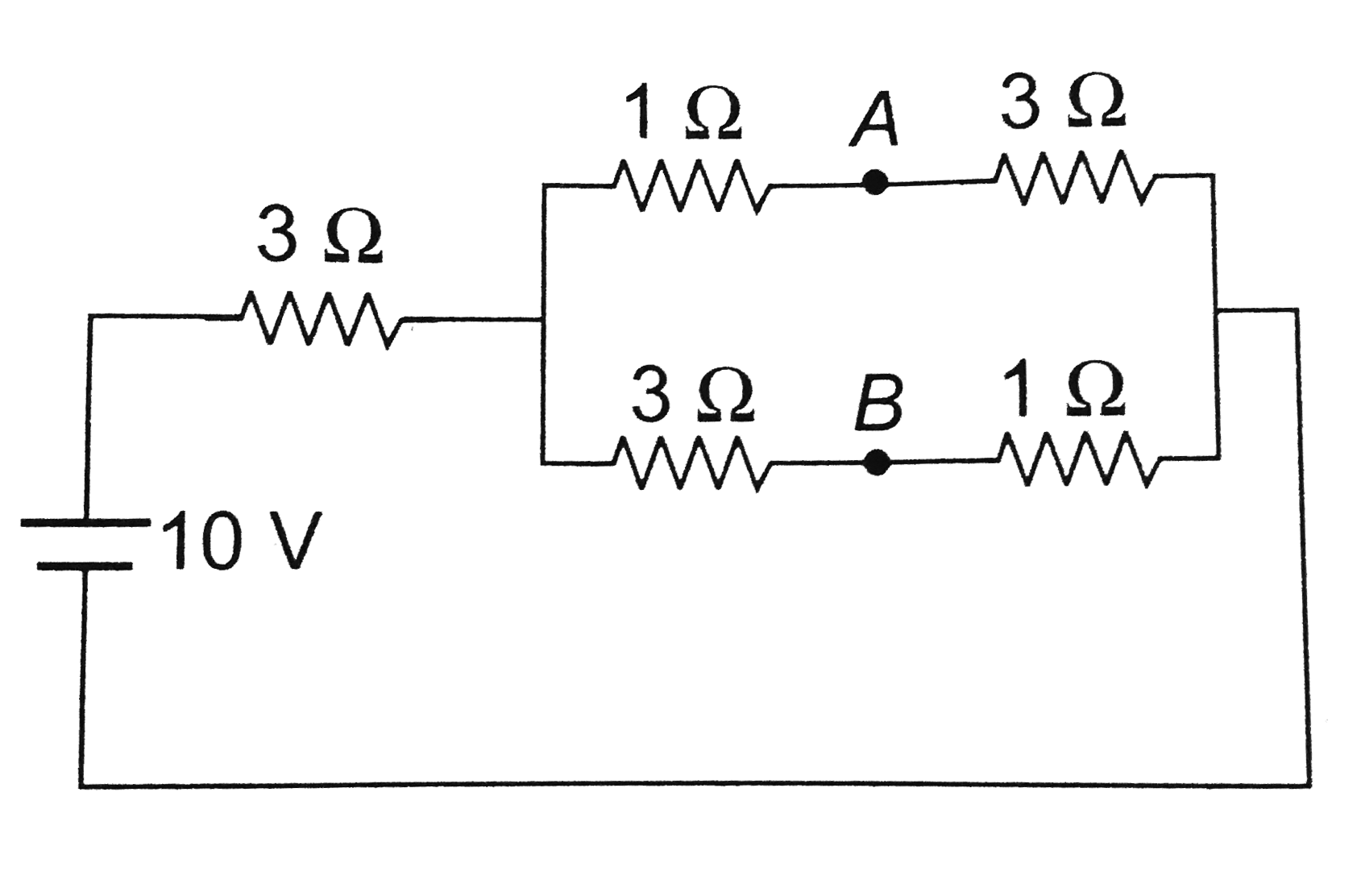
View Solution
