A particle of mass m and charge q is thrown with initial velocity v0 at an angle with the horizontal. In space there exist an electric field of strength E at angle β with the downward vertical away from the point of projection. Find the time of flight and range of projectile on horizontal ground
To solve the problem, we will break it down into several steps to find the time of flight and the range of the projectile.
Step 1: Identify the Initial Velocity Components
The initial velocity v0 is given at an angle α with the horizontal. We can resolve this into horizontal and vertical components:
- Horizontal component ux=v0cosα
- Vertical component uy=v0sinα
Step 2: Determine the Forces Acting on the Particle
Since the particle has charge q and is in an electric field E at an angle β with the downward vertical, we need to find the components of the electric force acting on the particle.
- The electric field has a component in the x-direction:
Fx=qEsinβ
- The electric field has a component in the y-direction:
Fy=qEcosβ
Step 3: Calculate the Acceleration Components
Using Newton's second law, we can find the acceleration due to the electric field:
- Acceleration in the x-direction:
ax=Fxm=qEsinβm
- Acceleration in the y-direction (including gravitational force):
ay=Fym−g=qEcosβm−g
Step 4: Calculate the Time of Flight
The time of flight T can be calculated using the formula:
T=2uyay
Substituting the values of uy and ay:
T=2(v0sinα)(qEcosβm−g)
Step 5: Calculate the Range of the Projectile
The range R can be calculated using the formula:
R=uxT+12axT2
Substituting the values of ux and ax:
R=(v0cosα)⎛⎜
⎜⎝2(v0sinα)(qEcosβm−g)⎞⎟
⎟⎠+12(qEsinβm)⎛⎜
⎜⎝2(v0sinα)(qEcosβm−g)⎞⎟
⎟⎠2
Final Expression for Range
After simplifying the above expression, we can derive the final formula for the range R.
Summary of Results
1. Time of Flight:
T=2(v0sinα)(qEcosβm−g)
2. Range:
R=(v0cosα)⎛⎜
⎜⎝2(v0sinα)(qEcosβm−g)⎞⎟
⎟⎠+12(qEsinβm)⎛⎜
⎜⎝2(v0sinα)(qEcosβm−g)⎞⎟
⎟⎠2
The initial velocity v0 is given at an angle α with the horizontal. We can resolve this into horizontal and vertical components:
- Vertical component uy=v0sinα
Since the particle has charge q and is in an electric field E at an angle β with the downward vertical, we need to find the components of the electric force acting on the particle.
Fx=qEsinβ
- The electric field has a component in the y-direction:
Fy=qEcosβ
Using Newton's second law, we can find the acceleration due to the electric field:
ax=Fxm=qEsinβm
- Acceleration in the y-direction (including gravitational force):
ay=Fym−g=qEcosβm−g
The time of flight T can be calculated using the formula:
T=2uyay
Substituting the values of uy and ay:
T=2(v0sinα)(qEcosβm−g)
The range R can be calculated using the formula:
R=uxT+12axT2
Substituting the values of ux and ax:
R=(v0cosα)⎛⎜
⎜⎝2(v0sinα)(qEcosβm−g)⎞⎟
⎟⎠+12(qEsinβm)⎛⎜
⎜⎝2(v0sinα)(qEcosβm−g)⎞⎟
⎟⎠2
After simplifying the above expression, we can derive the final formula for the range R.
1. Time of Flight:
T=2(v0sinα)(qEcosβm−g)
R=(v0cosα)⎛⎜
⎜⎝2(v0sinα)(qEcosβm−g)⎞⎟
⎟⎠+12(qEsinβm)⎛⎜
⎜⎝2(v0sinα)(qEcosβm−g)⎞⎟
⎟⎠2
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise 1.11videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise93videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs33videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
A2usinαgB2u2sinαgCusinαgDu2sinαg - Question 2 - Select One
A particle of mass 1kg is projected with an initial velocity 10ms−1 at an angle of projection 45∘ with the horizontal. The average torque acting on the projectile and the time at which it strikes the ground about the point of projection in newton meter is
A25B50C75D100 - Question 3 - Select One
A projectile is thrown with a velocity u0 at an angle θ with the horizontal. The ratio of the rate of change of speed w.r.t. time, at highest point to that at the point of projection, is
AgsinθB−gsinθCzeroDg
If a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionA projectile of mass (m) is thrown with velocity (u) from the ground at an angle of 60∘ with the horizontal. What is the magnitude of change in momentum between leaving and arriving back at the ground ?
View SolutionA particle of mass m is projected with an initial velocity U at an angle θ to the horizontal. The torque of gravity on projectile at maximum height about the point of projection is
View SolutionA particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity
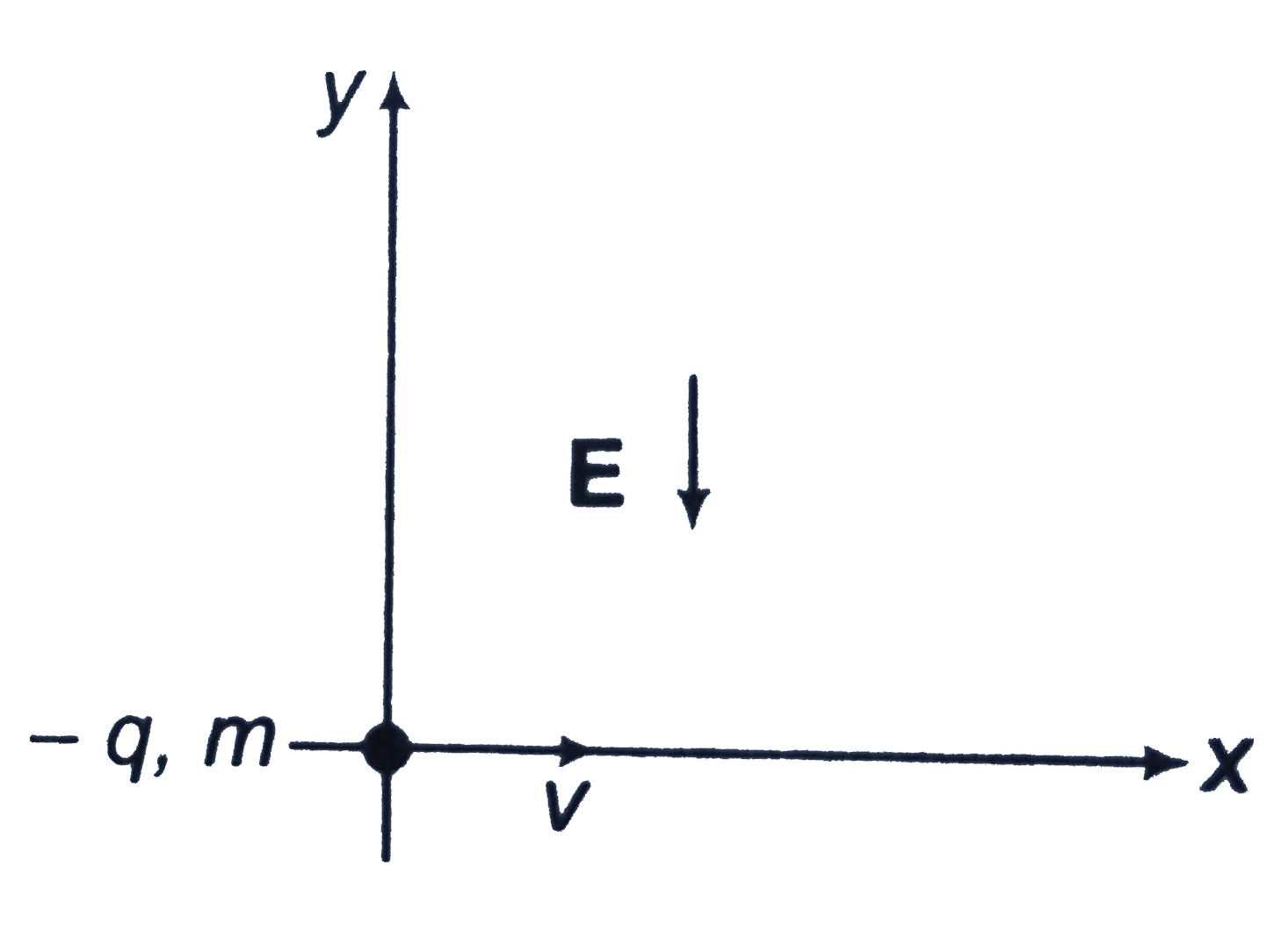 View Solution
View SolutionA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:
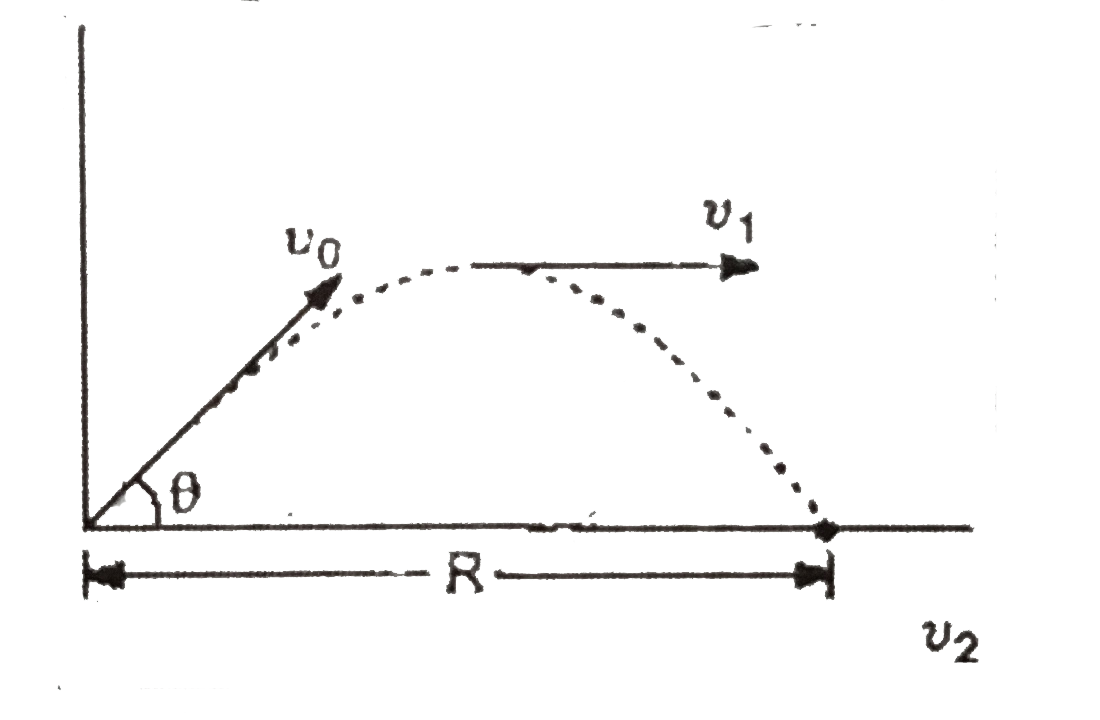 View Solution
View Solution

