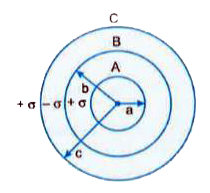
Three concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities $σ$ , $- σ$ and $σ$ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.

$a + b + c = 0$

$a + b = b$

$a + b = c$

$a = b + c$

Video Solution

Answer

Step by step video & image solution for Three concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities sigma, -sigma and sigma respectively. (i) Find the potential of the three shells A, B and C. (ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Three concentric spherical metallic spheres $A, B$ and $C$ of radii $a, b$ and $c (a < b < c)$ have surface charge densities $σ, - σ$ and $σ$ respectively.
AThe potential of shell $A$ :
$V_{A} = \frac{σ}{ε_{0}} (a + b + c)$
BThe potential of shell $B$ :
$V_{B} = \frac{σ}{ε_{0}} (\frac{a^{2}}{b} - b + c)$
CThe potential of shell $C$ :
$V_{C} = \frac{σ}{ε_{0}} (\frac{a^{2} - b^{2}}{c} + c)$
DAll options are correct
Question 2 - Select One
Three concentric metallic spherical shells $A, B$ and $C$ of radii $a, b$ and $c (a < b < c)$ have surface charge densities $- σ, + σ$ and -sigma $r e s p e c t i v e l y, t h e p o t e n t i a l o f s h e l l$ A is
A $(σ / ε_{0}) [a + b - c]$
B $(σ / ε_{0}) [a - b + c]$
C $(σ / ε_{0}) [b - a - c]$
Dnone
Question 3 - Select One
Three concentric metallic spherical shell $A, B$ and $C$ or radiin $a, b$ and C $(a < b > C)$ have surface charge densities $- sin g a m a, + σ$ , and $- a i g b a$ respectively .
The potential of shell $A$ is :
A $(σ / ɛ_{0}) [a + b - c]$
B $(σ / ɛ_{0}) [a + b - c]$
C $(σ / ɛ_{0}) [a + b - c]$
Dnone

PHYSICS GALAXY - ASHISH ARORA-ELECTROSTATICS-Numerical MCQs Single options Correct

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

Three concentric spherical metallic spheres A,B and C of radii a,b and c(a<b<c) have surface charge densities σ,−σ and σ respectively.

Three concentric metallic spherical shells A,B and C of radii a,band c(a<b<c) have surface charge densities −σ,+σand -sigma respectively,thepotentialofshellA is

Three concentric metallic spherical shell A,B and C or radiin a,b and C (a<b>C) have surface charge densities −singama,+σ, and −aigba respectively . The potential of shell A is :

PHYSICS GALAXY - ASHISH ARORA-ELECTROSTATICS-Numerical MCQs Single options Correct

Three concentric spherical metallic spheres $A, B$ and $C$ of radii $a, b$ and $c (a < b < c)$ have surface charge densities $σ, - σ$ and $σ$ respectively.

Three concentric metallic spherical shells $A, B$ and $C$ of radii $a, b$ and $c (a < b < c)$ have surface charge densities $- σ, + σ$ and -sigma $r e s p e c t i v e l y, t h e p o t e n t i a l o f s h e l l$ A is

Three concentric metallic spherical shell $A, B$ and $C$ or radiin $a, b$ and C $(a < b > C)$ have surface charge densities $- sin g a m a, + σ$ , and $- a i g b a$ respectively .
The potential of shell $A$ is :