The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
heat flows in the rod from high temperature to low temperature even if the rod has the non-unform cross sectional area
temperature gradient along length is same even if the rod has the non-unform cross sectional area
heat current is same even if the rod hasnon-unform cross sectional area
of the rod has uniform cross-sectional areathe temperature is same all the point at rod.
The correct Answer is:A, C
Step by step video, text & image solution for The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Comprehension type3videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Fill in the blanks type6videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - 241videos
THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
Similar Questions
One end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
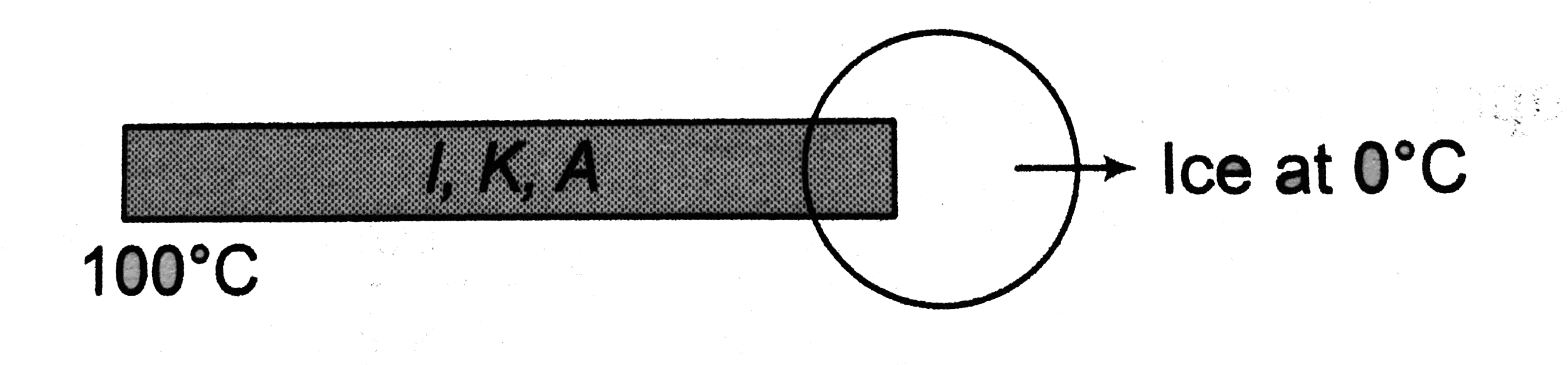 . View Solution
. View SolutionWhen two ends of a rod wrapped with cotton are maintained at different temperatures and after some time every point of the rod attains a constant temperature, then
View Solution
Knowledge Check
- Question 1 - Select One or More
Two ends of area A of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. At any point on the rod, the temperature gradient is dTdl. If I be the thermal current in the rod, then:
AI∝ABI∝dTdlCI∝A∘DI∝1(dTdl) - Question 2 - Select One or More
The two ends of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. The temperature gradientat any point on the rod is dθdl(equal to the difference in temperature per unit length). The heat flow per unit time per unit cross-section of the rod is l then which of the following statements is/are correct:
Adthηdl is the same for all points on the rodBI will decrease as we move from higher to lower temperatureCI∝k.dthηdlDAll the above options are incorrect - Question 3 - Select One
The two ends of uniform rod of thermal conductivity K are maintained at different but constant temperatre. The temperature gradient at any point on the rod is dθ/dx. The heat flow per unit time per unit cross-section of the rod is I.
(i) dθdx is the same for all point on the rod
(ii) I=KdθdxA(i) onlyB(ii) onlyC(i), (ii)Dnone
A rod of length L and uniform cross-sectional area has varying thermal conductivity which changes linearly from 2K at end A to K at the other end B. The ends A and B of the rod are maintained at constant temperture 100∘C and 0∘C, respectively. At steady state, the graph of temperture : T=T(x) where x= distance from end A will be
View SolutionThe ends of a cylinder steel rod are maintained at two different temperatures. The rod conducts heat from one end to the other at a rate of 10 cal/ s. At what rate would a steel rod twice as long and twice the diameter conduct heat between the same two temperatures?
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
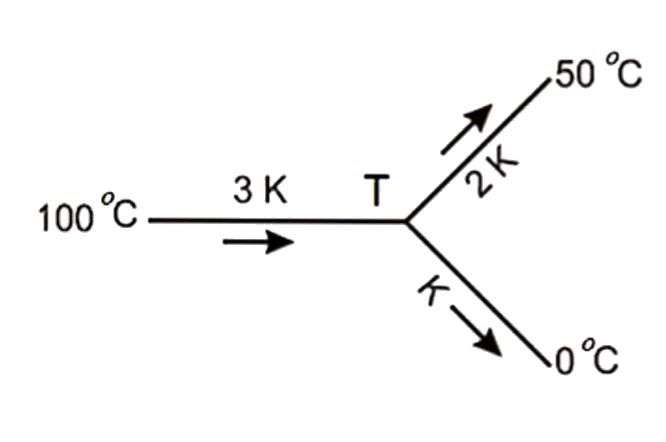 View Solution
View SolutionWhen two ends of a rod wrapped with cotton are maintained at differences and after some time every point of the rod attains a constant temperature, then
View SolutionA cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system ?
View Solution

