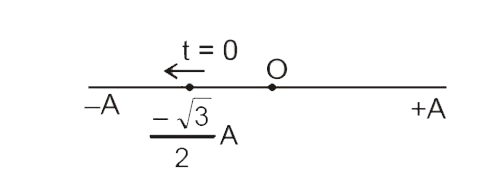
A particles starts from point x=−√32A and move towards negative extrene as shown . If the time period of oscillation is T , them

The equation of the SHM is x=Asin(2πT+4π3)
The time taken by the particle tto go directly from its initial position to negative extreme is T12
The time taken by the particle to reach at mean position is T3
The equation of the SHM is x=Asin(2πT+π3)
The correct Answer is:A, B, C
Step by step video, text & image solution for A particles starts from point x=-sqrt(3)/(2) A and move towards negative extrene as shown . If the time period of oscillation is T , them by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type3videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type2videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
A particle starts from point x=−√32A and move towards negative extreme as shown
(a) Find the equation of the SHM.
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
 View Solution
View SolutionA particle starts from point x=−√32A and move towards negative extreme as shown,
_S01_011_Q01.png)
(a) Find the equation of the SHM
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.View Solution
Knowledge Check
- Question 1 - Select One
A particle moves such that acceleration is given by a=−4x. The period of oscillation is
AπB2πC1πD2π - Question 2 - Select One or More
A particle starts from a point P at a distance of A/2 from the mean position O& travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of motion of particle is :
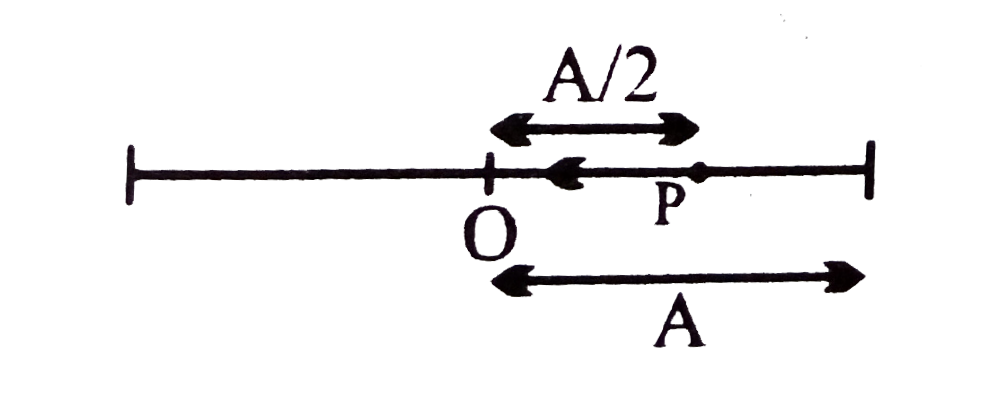 AX=Asin(2πTt+π6)BX=Asin(2πTt+5π6)CX=Acos(2πTt+π6)DX=Acos(2πTt+π3)
AX=Asin(2πTt+π6)BX=Asin(2πTt+5π6)CX=Acos(2πTt+π6)DX=Acos(2πTt+π3) - Question 3 - Select One or More
A particle starts from a point P at a distance of A/2 from the mean position O and travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of the motion of particle is
 Ax=Asin(2πTt+π6)Bx=Asin(2πTt+5π6)Cx=Acos(2πTt+π6)Dx=Acos(2πTt+π3)
Ax=Asin(2πTt+π6)Bx=Asin(2πTt+5π6)Cx=Acos(2πTt+π6)Dx=Acos(2πTt+π3)
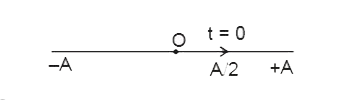
A particle starts from A/2 and moves towards positive extreme as shown below. Find the equation of the SHM. Given amplitude of SHM is A.
 View Solution
View SolutionA particle moves so that its acceleration a is give by a=bn where x is displacement from equilibrium position and b is non negative real constant the time period of oscillation of the particle is
View SolutionA particle moves so that its acceleration a is give by a=bn where x is displacement from equilibrium position and b is non negative real constant the time period of oscillation of the particle is
View SolutionA particle starts from origin and moving along x−axis. Whose v−t graph is as shown . Choose the INCORRECT statement :
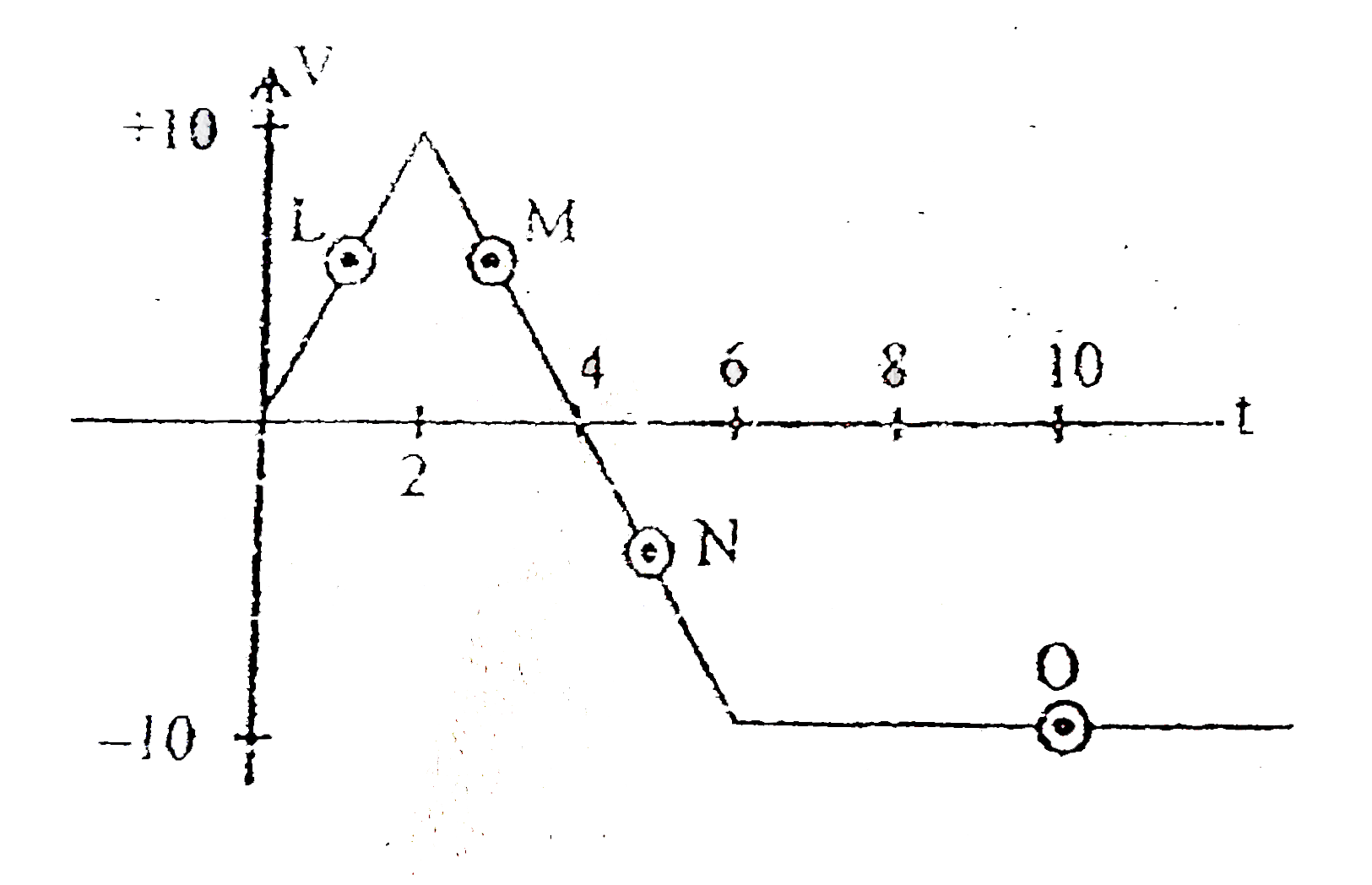 .View Solution
.View SolutionA particle starts from rest x = - 2.25 m and moves along the x - axis with the v - t graph as shown. The time when the particle crosses the origin is :
 View Solution
View Solution

