The temperature of a definite amount of an ideal monoatomic gas becomes four times in a reversible process for which heat exchange is zero. Which of the following is correct relation between the final and initial parameteres of gas?
The correct Answer is:B
To solve the problem, we need to analyze the behavior of an ideal monoatomic gas undergoing a reversible process where the temperature increases to four times its initial value, and there is no heat exchange (adiabatic process).
1. Identify Initial and Final Conditions:
- Let the initial temperature be T1.
- The final temperature is given as T2=4T1.
- We denote the initial volume as V1 and the final volume as V2.
- The initial pressure is P1 and the final pressure is P2.
2. Use the Adiabatic Condition:
- For an ideal gas undergoing an adiabatic process, we can use the relation:
PVγ=constant
- For a monoatomic gas, γ=53.
3. Apply the Adiabatic Relation:
- From the adiabatic condition, we have:
P1Vγ1=P2Vγ2
- Rearranging gives:
P2P1=(V1V2)γ
4. Use the Ideal Gas Law:
- The ideal gas law states that:
PV=nRT
- For two states of the gas, we can write:
P1V1T1=P2V2T2
- Rearranging gives:
P2P1=T2V1T1V2
5. Substitute Known Values:
- Substitute T2=4T1 into the equation:
P2P1=4T1V1T1V2=4V1V2
6. Combine the Two Relations:
- Now we have two expressions for P2P1:
1. From the adiabatic relation: P2P1=(V1V2)53
2. From the ideal gas law: P2P1=4V1V2
7. Set the Two Expressions Equal:
- Equating the two expressions:
(V1V2)53=4V1V2
8. Solve for Volume Ratio:
- Let x=V1V2:
x53=4x⟹x53−1=4⟹x23=4⟹x=432=8
- Thus, V1V2=8 or V1=8V2.
9. Find Pressure Relation:
- Substitute V1=8V2 back into the pressure relation:
P2P1=4⋅8V2V2=32⟹P2=32P1
Final Relations:
- The correct relations are:
- V1=8V2
- P2=32P1
- Let the initial temperature be T1.
- The final temperature is given as T2=4T1.
- We denote the initial volume as V1 and the final volume as V2.
- The initial pressure is P1 and the final pressure is P2.
- For an ideal gas undergoing an adiabatic process, we can use the relation:
PVγ=constant
- For a monoatomic gas, γ=53.
- From the adiabatic condition, we have:
P1Vγ1=P2Vγ2
- Rearranging gives:
P2P1=(V1V2)γ
- The ideal gas law states that:
PV=nRT
- For two states of the gas, we can write:
P1V1T1=P2V2T2
- Rearranging gives:
P2P1=T2V1T1V2
- Substitute T2=4T1 into the equation:
P2P1=4T1V1T1V2=4V1V2
- Now we have two expressions for P2P1:
1. From the adiabatic relation: P2P1=(V1V2)53
2. From the ideal gas law: P2P1=4V1V2
- Equating the two expressions:
(V1V2)53=4V1V2
- Let x=V1V2:
x53=4x⟹x53−1=4⟹x23=4⟹x=432=8
- Thus, V1V2=8 or V1=8V2.
- Substitute V1=8V2 back into the pressure relation:
P2P1=4⋅8V2V2=32⟹P2=32P1
- The correct relations are:
- V1=8V2
- P2=32P1
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The temperture of a definite amount of an ideal monoatomic gas becomes four times in a reversible
process for which heat exchange is zero. Which of the following is correct relation between the final and
initial parameters of gas ?AVf=8ViBPf=32PiCVf=16ViDPf=116Pi - Question 2 - Select One
One mole of an ideal monoatomic gas under goes a process V=aT2. The temperature of the gas increases by 100K. Which of the following is incorrect ?
Athe work done by the gas in the process is 200R JouleBthe molar heat capacity for the process is 7R2Cfor the process PT2= constantDfor the process coefficient of volume expansion is γ=2T - Question 3 - Select One
Which of the following graph is correct reversible adiabatic process for an ideal gas:
A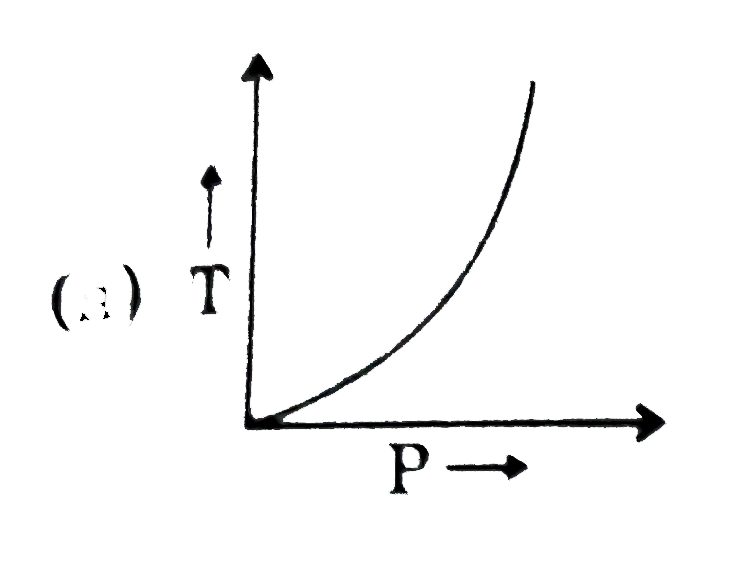 B
B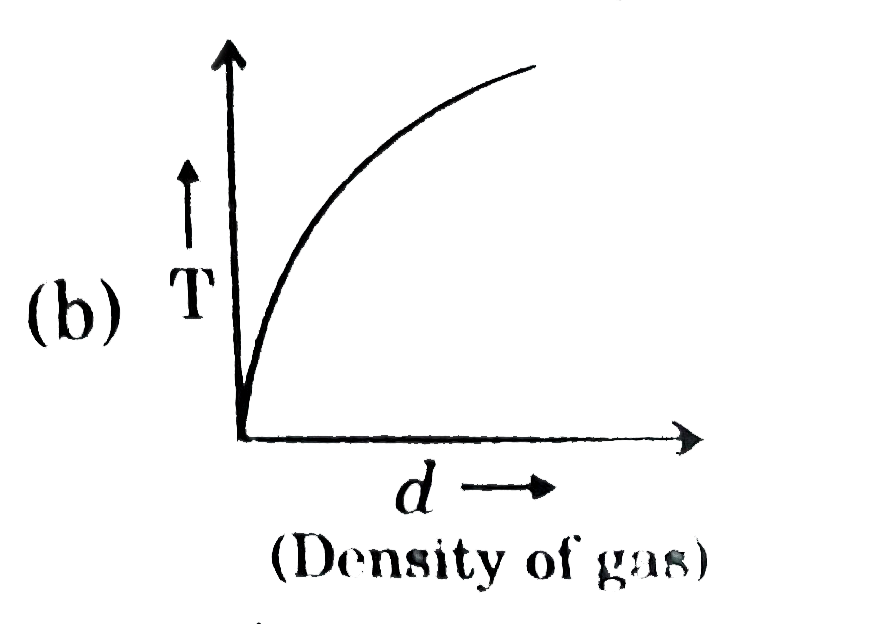 C
C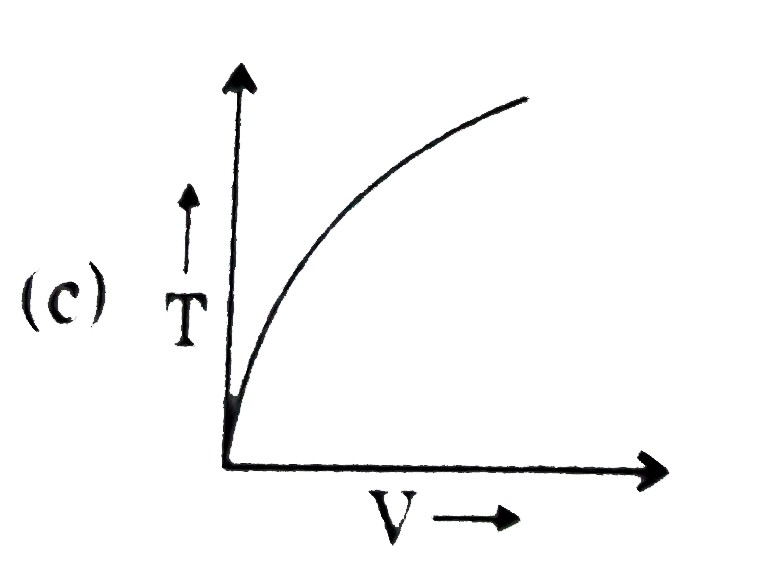 D
D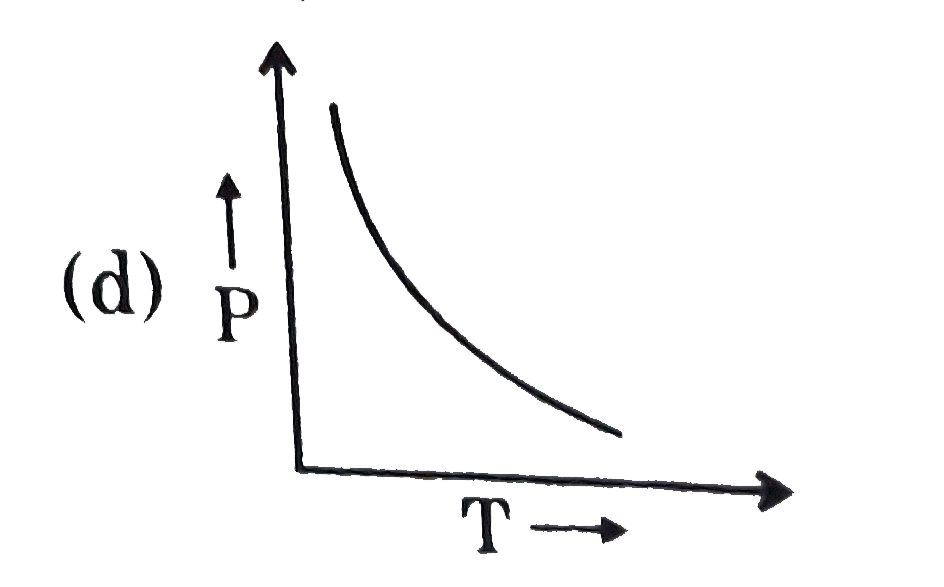
Which of the following curve is correct for a given amount of an ideal gas at constant pressure?
View SolutionWhich of the following is true for reversible adiabatic process involving an ideal gas ?
View SolutionWhich of the following curve is incorrect for given amount of an ideal gas at constant temperature ?
View SolutionIn a constant pressure process, for 5mole of an ideal monoatomic gas, the temperature of gas increased form 300K→500k. Which of the following is incorrect reagarding the process?
View Solution2 mole of an ideal monoatomic gas undergoes a reversible process for which PV2=C. The gas is expanded from initial volume of 1 L to final volume of 3 L starting from initial temperature of 300 K. Find ΔH for the process :
View Solution

