Boron exist in different allotropic forms .All allotropic fropm contains icosahedral units (icosahedral is a regular shape with 12 corners and 20 faces ) with boron atoms at all 12 corners and all bonds are equivalent .

Calculate ΔH (n KJ) per mole of boron atoms formating gaseous icosahedron if ΔHBE(B−B)=200KJ/mol:
1000
600
500
250
The correct Answer is:c
Topper's Solved these Questions
Similar Questions
Boron exist in different allotropic forms. All allotropic form contains icosahedral units (icosahedral is regular shape with 12 corner & 20 faces) with boron atoms at all 12 corners and all bonds are equivalent.
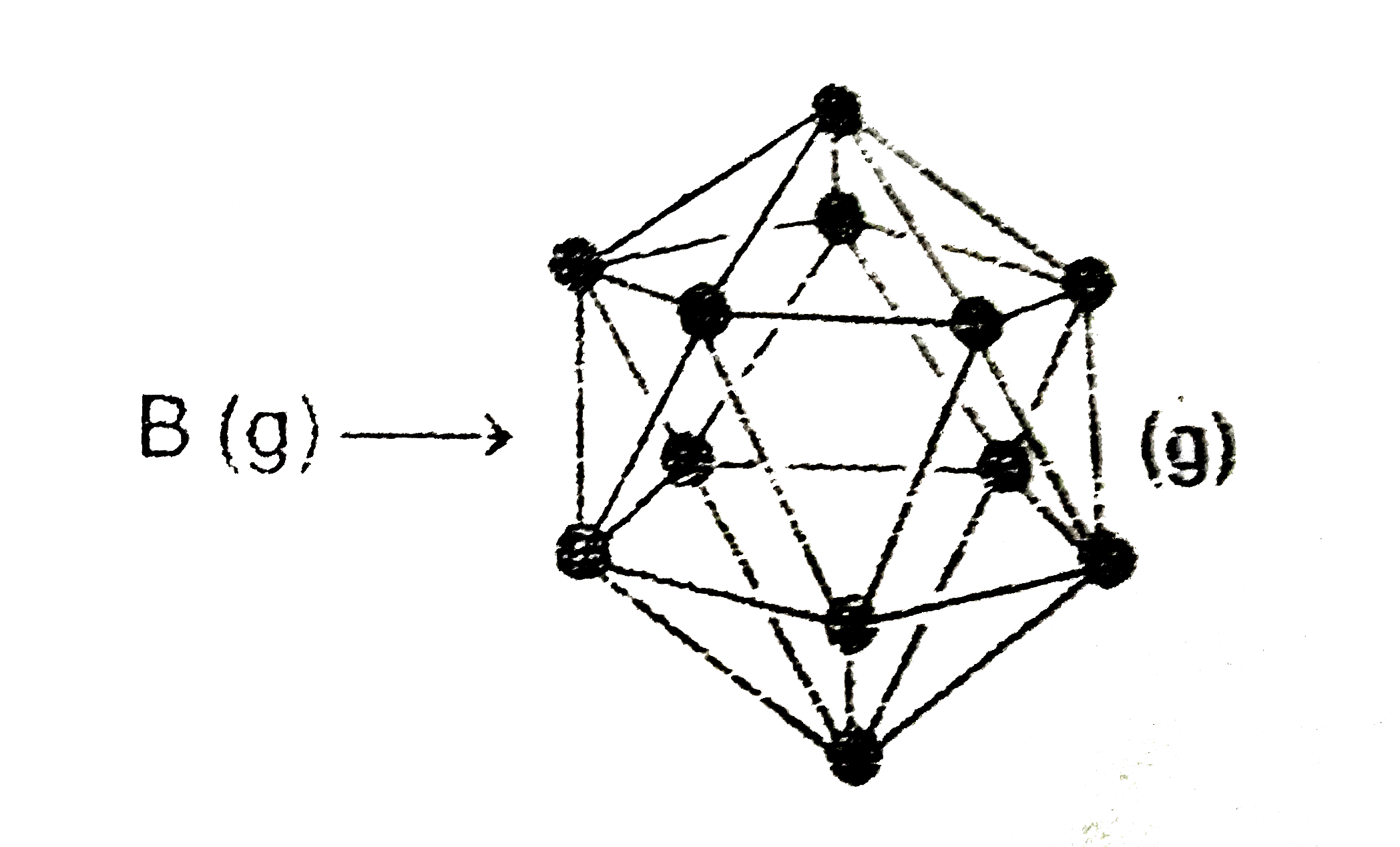
Calculate heat evolved at constant pressure (in KJ) per mole of boron atoms undergoing above change it ΔHBE(B−B)=200KJ/mol. Report you answer after dividing by 100
View SolutionBoron exist in different allotropic forms. All allotropic form contains icosahedral units (icosahedral is regular shape with 12 corner & 20 faces) with boron atoms at all 12 corners and all bonds are equivalent.
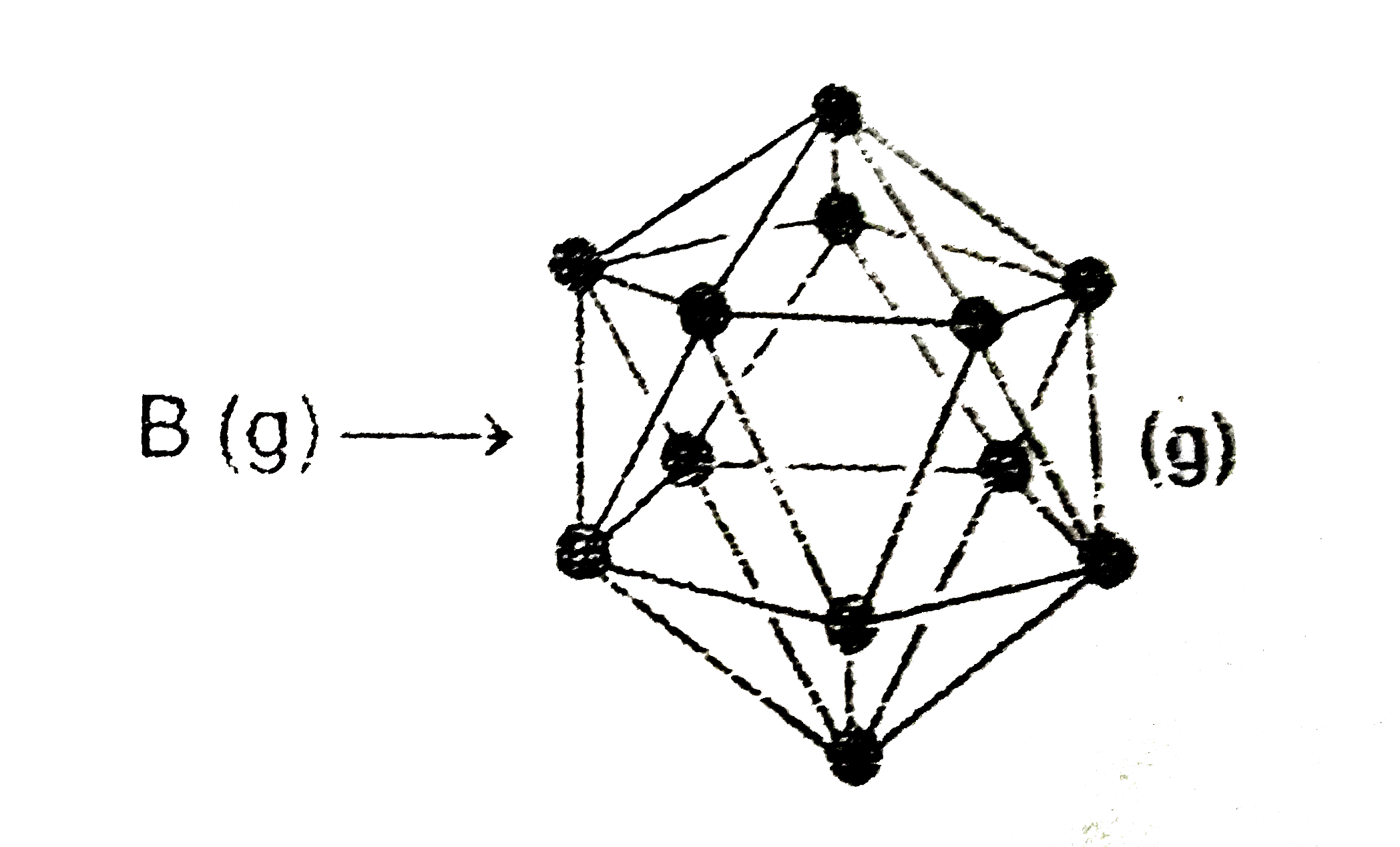
Calculate heat evolved at constant pressure (in KJ) per mole of boron atoms undergoing above change it ΔHBE(B−B)=200KJ/mol. Report you answer after dividing by 100
View Solution
Knowledge Check
One of the allotropic form of boron is α− rhombohedral boron. Number of faces and corners in its basic building B12 icosahedral unit are:
A20 and 12 respectivelyB12 and 20 respectivelyC12 and 12 respectivelyD20 and 20 respectivelyIn the crystalline solids the smallest repeating part in the lattice is known as unit cell. The unit cells are described as simple (points at all corners), body centred (points at all the corners and it the centre), face centred (points at all the corners and centre of all faces), and end centred (points at all hte corners and centres of two opposite and faces) unit cells. In two common tyupes of packing ccp and hcp, 26% of space is left unoccupied in the form of interstitial sites. For the stable ionic crystalline structures, there is difinite radius ratio limit for a cation to fit perfectly in the lattice of anions, called radius ratio rule. This also defines the coordination number of an ion, which is the number of nearest neighbours of opposite charges. This depeds upon the ratio of radii of two types of ions, r+/r−. This ratio for coordination numbers 3,4,6,and 8 is respectively 0.155 - 0.225, 0.225 - 0.414, 0.414 - 0.732 and 0.732 - 1 respectively.
A face centred lattice a metal M and a body centred cubic lattice of metal N contain same number of 2.25×1022 unit cells. If density of M is twice than that of N, the ratio between the number of atoms per unit cell isA4:1B1:1C2:1D1:4In the crystalline solids the smallest repeating part in the lattice is known as unit cell. The unit cells are described as simple (points at all corners), body centred (points at all the corners and it the centre), face centred (points at all the corners and centre of all faces), and end centred (points at all hte corners and centres of two opposite and faces) unit cells. In two common tyupes of packing ccp and hcp, 26% of space is left unoccupied in the form of interstitial sites. For the stable ionic crystalline structures, there is difinite radius ratio limit for a cation to fit perfectly in the lattice of anions, called radius ratio rule. This also defines the coordination number of an ion, which is the number of nearest neighbours of opposite charges. This depeds upon the ratio of radii of two types of ions, r+/r−. This ratio for coordination numbers 3,4,6,and 8 is respectively 0.155 - 0.225, 0.225 - 0.414, 0.414 - 0.732 and 0.732 - 1 respectively.
The number of atoms per unit cell in simple (s), body centred(b) , face centred (f) and end centred (e) unit cell decreases asAf > b > e > sBf > b = e > sCb > f > s = eDf > b > e = s
In the icosahedron of B12 unit each boron atom is bonded to how many boron atoms.
View SolutionOne of the allotropic form of boron is α− rhombohedral boron. Number of faces and corners in its basic building B12 icosahedral unit are:
View SolutionThe simplest formula of a compound whose cubic unit cell contains A atoms on all corners, B atoms on alternate face centre andC atoms on one third of edge centre, is
View SolutionThe simplest formula of a compound whose cubic unit cell contains A atoms on all corners, B atoms on alternate face centre andC atoms on one third of edge centre, is
View SolutionAtoms of element A and B form an HCP lattice such that atoms of A are present at corners of the unit cell and atoms of B are present at the centers of both the hexagonal faces as well as inside the unit cell. All the tetrahedral voids are occupied by atoms of element C and all the octahedral voids are occupied by atoms of element D. Find out the formula of the crystalline solid.
View Solution
