One of the allotropic form of boron is α− rhombohedral boron. Number of faces and corners in its basic building B12 icosahedral unit are:
20 and 12 respectively
12 and 20 respectively
12 and 12 respectively
20 and 20 respectively
The correct Answer is:A
To solve the problem regarding the number of faces and corners in the basic building unit of alpha-rhombohedral boron, which consists of the B12 icosahedral unit, we can follow these steps:
1. Understanding the Structure:
- The alpha-rhombohedral boron consists of a basic building unit known as the B12 icosahedral unit. This unit is crucial for understanding the geometry of the boron allotrope.
2. Identifying the Icosahedral Unit:
- An icosahedron is a polyhedron with 20 faces, 12 vertices (corners), and 30 edges. This geometric shape is significant in the arrangement of boron atoms in the alpha-rhombohedral structure.
3. Counting the Faces:
- In the B12 icosahedral unit, there are 20 triangular faces. Each face corresponds to a triangular arrangement of boron atoms.
4. Counting the Corners:
- The B12 icosahedral unit has 12 corners (vertices). Each corner represents a position where a boron atom is located.
5. Final Summary:
- Therefore, for the B12 icosahedral unit in alpha-rhombohedral boron:
- Number of Faces = 20
- Number of Corners = 12
Conclusion:
The number of faces and corners in the B12 icosahedral unit of alpha-rhombohedral boron is:
- Faces: 20
- Corners: 12
- The alpha-rhombohedral boron consists of a basic building unit known as the B12 icosahedral unit. This unit is crucial for understanding the geometry of the boron allotrope.
- An icosahedron is a polyhedron with 20 faces, 12 vertices (corners), and 30 edges. This geometric shape is significant in the arrangement of boron atoms in the alpha-rhombohedral structure.
- In the B12 icosahedral unit, there are 20 triangular faces. Each face corresponds to a triangular arrangement of boron atoms.
- The B12 icosahedral unit has 12 corners (vertices). Each corner represents a position where a boron atom is located.
- Therefore, for the B12 icosahedral unit in alpha-rhombohedral boron:
- Number of Faces = 20
- Number of Corners = 12
The number of faces and corners in the B12 icosahedral unit of alpha-rhombohedral boron is:
- Faces: 20
- Corners: 12
Similar Questions
Boron exist in different allotropic forms. All allotropic form contains icosahedral units (icosahedral is regular shape with 12 corner & 20 faces) with boron atoms at all 12 corners and all bonds are equivalent.
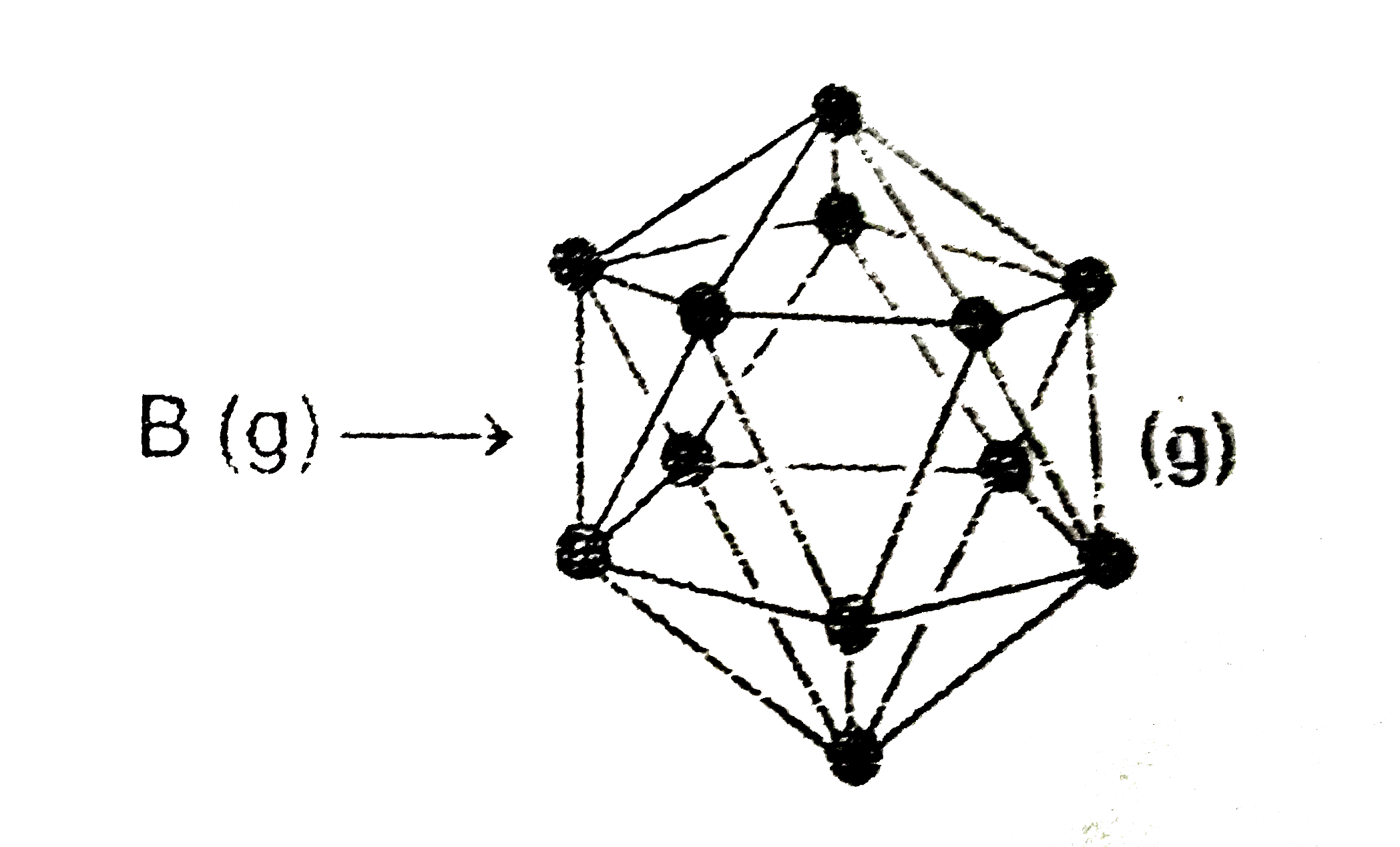
Calculate heat evolved at constant pressure (in KJ) per mole of boron atoms undergoing above change it ΔHBE(B−B)=200KJ/mol. Report you answer after dividing by 100View SolutionIron adopts two different crystalline allotropic forms one at 1183 K and other one below 1183 K, which differ in structural units as bcc and fcc are known as α and γ forms.. What would be the ratio of densities of these two forms (γ and α ) ? Assume inter atomic distance remains same.
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and Y atoms are at the face centres. One atoms X is misssing from the corner.
a. Calculate (i). Zeff' (ii). total number of the atoms in the cube, and (iii). formula of the compound.
b. If alll the atoms are removed from one of the faces of the cube containing atoms at corners, as in (a) above, calculate (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.View SolutionIn a face centered lattice of X and Y, X atoms are present at the corners while Y atoms are at face centres.
(a) What is the formula of the compound ?
(b) What would be the formula of the compound if (i) one of the X atoms is missing from a corner in each unit cell
(ii) one of the X atoms at from a corner is replaced by Z atom. (also monovalent) ?View SolutionIn a solid 'AB' having rock salt arrangement (NaCl structure), 'A' atoms occupy the corners and face center of the cubic unit cell. 'B' atoms occupies all octahedral voids of the unit cell. If all the face - centered atoms along one of the axes are removed, then the resultant stoichiometry of the solid is
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corners of the cube of and two atoms (Y) are at each body diagonal of the cube.
a. Calculate: (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
b. If all atoms form one body diagonal of the cube except corners are removed, calculate: (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body centre and at the edge centre of the cube.
a. Celculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the body diagonals of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
c. If all the atoms from the diagonals of the one of the face of the cube are removed, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of t he cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from one of the axes passing through one of the face centres of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.View SolutionA currrent I is passed through a silver strip of width d and area of cross section A. The number of free electrons per unit volume is n. (a) Find the drift velocity v of the electrons. (b) If a magnetic field B exists in the region as shown in what is the average magnetic force on the free electrons? (c) Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will be the potential diference developed across the width of the conductor due to the electron- accumulation? The appearance of a transverse emf, when a current-carrying wire is placed in a magnetic field, is called hall effect.
 View Solution
View SolutionIn the fcc arrangement of A and B atoms whose A atoms are at corners of the unit cell and B are at the face centres one of the A atom is missing from one corner in each unit cell. What is the simplest formula of the compound?
View SolutionIn a f.c.c. arrangement of A and B atoms, where A atoms are at the corners of the unit cell and B atoms at the face − centres, one of the A atom is missing from one corner in each unit cell. The formula of compound is :
View Solution

