Three identical solid spheres move down three incline A,B and C are all of the same dimensions. A is without friction, the friction between B and a sphere is sufficient to cause rolling without slipping, the friction between C and a sphere causes rolling with slipping. The kinetic energies, of A,B,C at the bottom of the inclines are EA,EB,EC.
EA=EB=EC
EA=EB>EC
EA>EB>EC
EA>EB=EC
The correct Answer is:B
Step by step video, text & image solution for Three identical solid spheres move down three incline A, B and C are all of the same dimensions. A is without friction, the friction between B and a sphere is sufficient to cause rolling without slipping, the friction between C and a sphere causes rolling with slipping. The kinetic energies, of A, B, C at the bottom of the inclines are E_(A),E_(B),E_(C). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE
41 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - COMPREHENSION_TYPE
29 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN
12 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

Force of friction between sphere and plank is
View SolutionA hollow sphere rolls down a rough inclined plane whose angle of inclination is θ, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [μ = coefficient of friction between the hollow sphere and inclined plane]
View Solution
Knowledge Check
A hollow sphere rolls down a 30∘ incline of length 6m without slipping. The speed of centre of mass at the bottom of plane is
A6ms−1B3ms−1C6√2ms−1D3√3ms−1What is the minimum coefficient of friction for a solid sphere to roll without slipping on an inclined plane of inclination θ ?
A27tanθB13tanθC12tanθD25tanθA solid sphere starts from rest at the top of an incline of height h and length l, and moves down. The force of friction between the sphere and the incline is F. This is insufficient to prevent slipping. The kinetic energy of the sphere at the bottom of the incline is W.
AThe work done against the force of friction is Fl.BThe heat produced is Fl.CW=mgh-FlDW>(mgh-Fl)
A solid sphere is rolling without slipping on a horizontal plane. The ratio of its rotational kinetic energy and translational kinetic energy is
View SolutionA solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. The smallest kinetic energy at the bottom of the incline will be achieved by
View SolutionA rolling body is kept on a plank B. There is sufficient friction between A and B and no friction between B and the inclined plane. Then body:
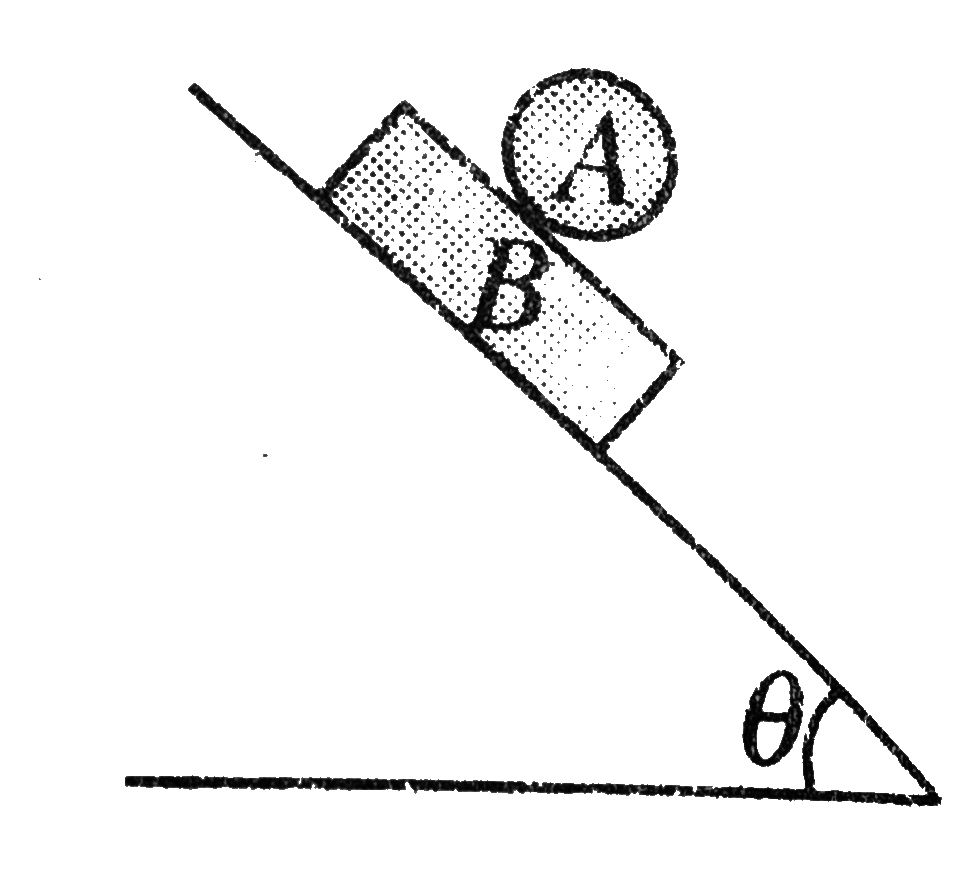
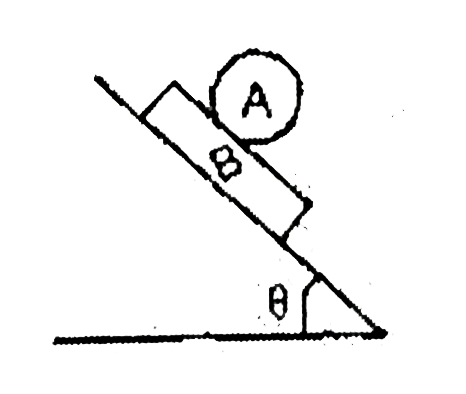
View SolutionA rolling body is kept on a plank B. There is sufficient friction between A and B and no friction between B and the incline,d plane. Then body:
View SolutionA plane srface is inclined at an angle θ. A cube slides down the plane and a solid sphere rolls down the plane without slipping. The ratio of the acceleration of the cube to that of the sphere is
View Solution
