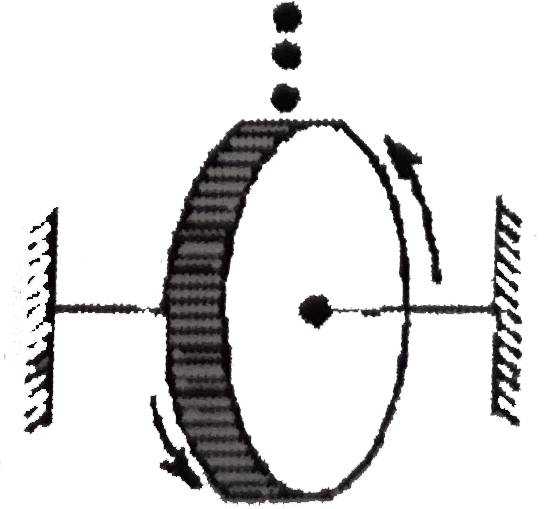
A disc of mass m0 rotates freely about a fixed horizontal axis through its center. A thin cotton pad is fixed to its rim, which can absorb water. The mass of water dripping onto the pad is μ per second. After what time will the angular velocity of the disc get reduced to half of its initial value:
2m0μ
3m0μ
m0μ
m02μ
The correct Answer is:D
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE41videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - COMPREHENSION_TYPE29videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.View Solution-
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.View Solution
Knowledge Check
- Question 1 - Select One
A disc of mass m0 rotates freely about a fixed horizontal axis through its centre. A thin cotton pad is fixed to its rim, which can absorb water. The mass of water dripping onto the pad is n per second: After what time will the angular velocity of the disc get reduced to half of its initial value ?
A2m0μB3m0μCm0μDm02μ - Question 2 - Select One
A disc of mass m0 rotates freely about a fixed horizontal axis passing through its centre. A thin cotton pad is fixed to its rim, which can absorb water. The mass of water dripping onto the pad per unit time is μ. After what time will the angular velocity of the disc get reduced to half its initial value?A2m0μB3m0μCm0μDm02μ - Question 3 - Select One or More
A horizontal disc rotates freely about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is now gently placed on the disc. After some time, the two rotate with a common angular velocity, then
Asome friction exists between the disc and the ringBthe angular momentum of the 'disc plus ring' is conservedCthe final common angular velocity is (23)rd of the initial angular velocity of the discD(23)rd of the initial kinetic energy changes to heat
A horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.View SolutionA horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.View SolutionA disc is free to rotate about a smooth horizontal axis passing through its centre of mass. A particle is fixed at the top of the disc. A slight push is given to the disc and it starts rotating. During the process.
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim.
The angular velocity of the disc after the particle sticks to it isView Solution