A horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.
To solve this problem, we will use the principles of conservation of angular momentum and the work-energy theorem. Let's break it down step by step.
Step 1: Understand the system
We have a uniform disc of mass M and radius R that is rotating with an initial angular velocity ω0. A small body of mass m is initially at the edge of the disc and can slide towards the center along a radial guide. We need to find the final angular velocity of the system when the body reaches the center and the work done by the force F.
Step 2: Calculate the initial moment of inertia
The initial moment of inertia Ii of the system can be calculated as the sum of the moment of inertia of the disc and the moment of inertia of the mass m at the edge of the disc.
Ii=Idisc+Imass=12MR2+mR2
Step 3: Calculate the final moment of inertia
When the mass m is pulled to the center of the disc, its distance from the axis of rotation becomes zero. Therefore, the final moment of inertia If is just that of the disc:
If=Idisc=12MR2
Step 4: Apply conservation of angular momentum
According to the conservation of angular momentum, the initial angular momentum Li must equal the final angular momentum Lf:
Li=Lf
Iiω0=Ifωf
Substituting the expressions for Ii and If:
(12MR2+mR2)ω0=(12MR2)ωf
Step 5: Solve for the final angular velocity ωf
Rearranging the equation to solve for ωf:
ωf=(12MR2+mR2)ω012MR2
ωf=(M+2mM)ω0
Step 6: Calculate the work done by the force F
Using the work-energy theorem, the work done W is equal to the change in kinetic energy of the system:
W=Kf−Ki
Where Ki and Kf are the initial and final kinetic energies respectively:
Ki=12Iiω20=12(12MR2+mR2)ω20
Kf=12Ifω2f=12(12MR2)((M+2m)Mω0)2
Calculating Kf:
Kf=12(12MR2)(M+2m)2M2ω20
Now, substituting Ki and Kf into the work done equation:
W=(12(12MR2(M+2m)2M2−(12MR2+mR2))ω20)
Final Answers
(a) The final angular velocity ωf is:
ωf=(M+2mM)ω0
(b) The work done W is:
W=12R2ω20((M+2m)2M2−(12+mM))
We have a uniform disc of mass M and radius R that is rotating with an initial angular velocity ω0. A small body of mass m is initially at the edge of the disc and can slide towards the center along a radial guide. We need to find the final angular velocity of the system when the body reaches the center and the work done by the force F.
The initial moment of inertia Ii of the system can be calculated as the sum of the moment of inertia of the disc and the moment of inertia of the mass m at the edge of the disc.
When the mass m is pulled to the center of the disc, its distance from the axis of rotation becomes zero. Therefore, the final moment of inertia If is just that of the disc:
According to the conservation of angular momentum, the initial angular momentum Li must equal the final angular momentum Lf:
Rearranging the equation to solve for ωf:
Using the work-energy theorem, the work done W is equal to the change in kinetic energy of the system:
(a) The final angular velocity ωf is:
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionCalculate the moment of inertia of a.unifprm disc of mass 0.4 kg and radius 0.1m about an axis passing through its edge and perpendicular to the plane of die disc ?
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
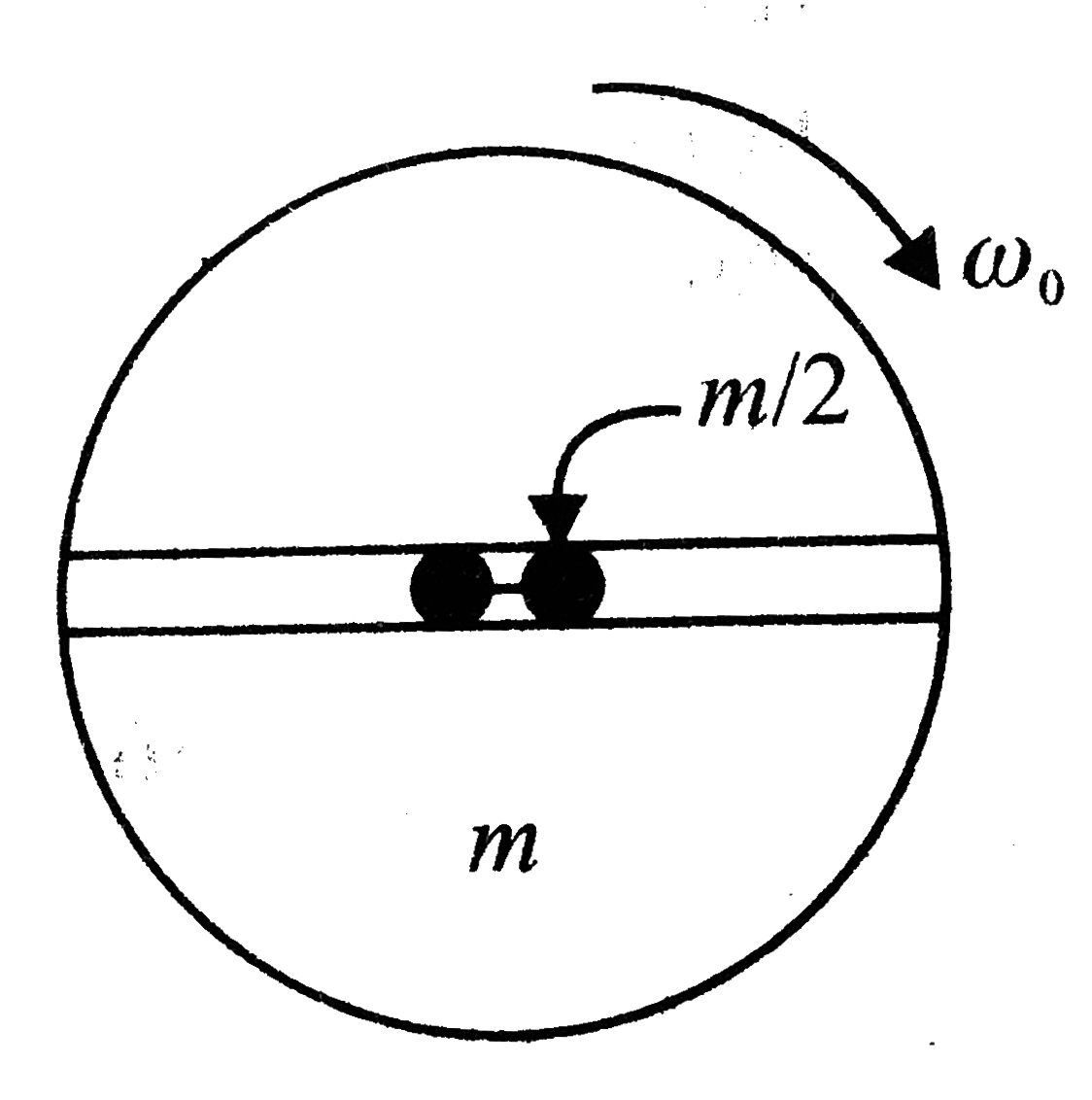
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is
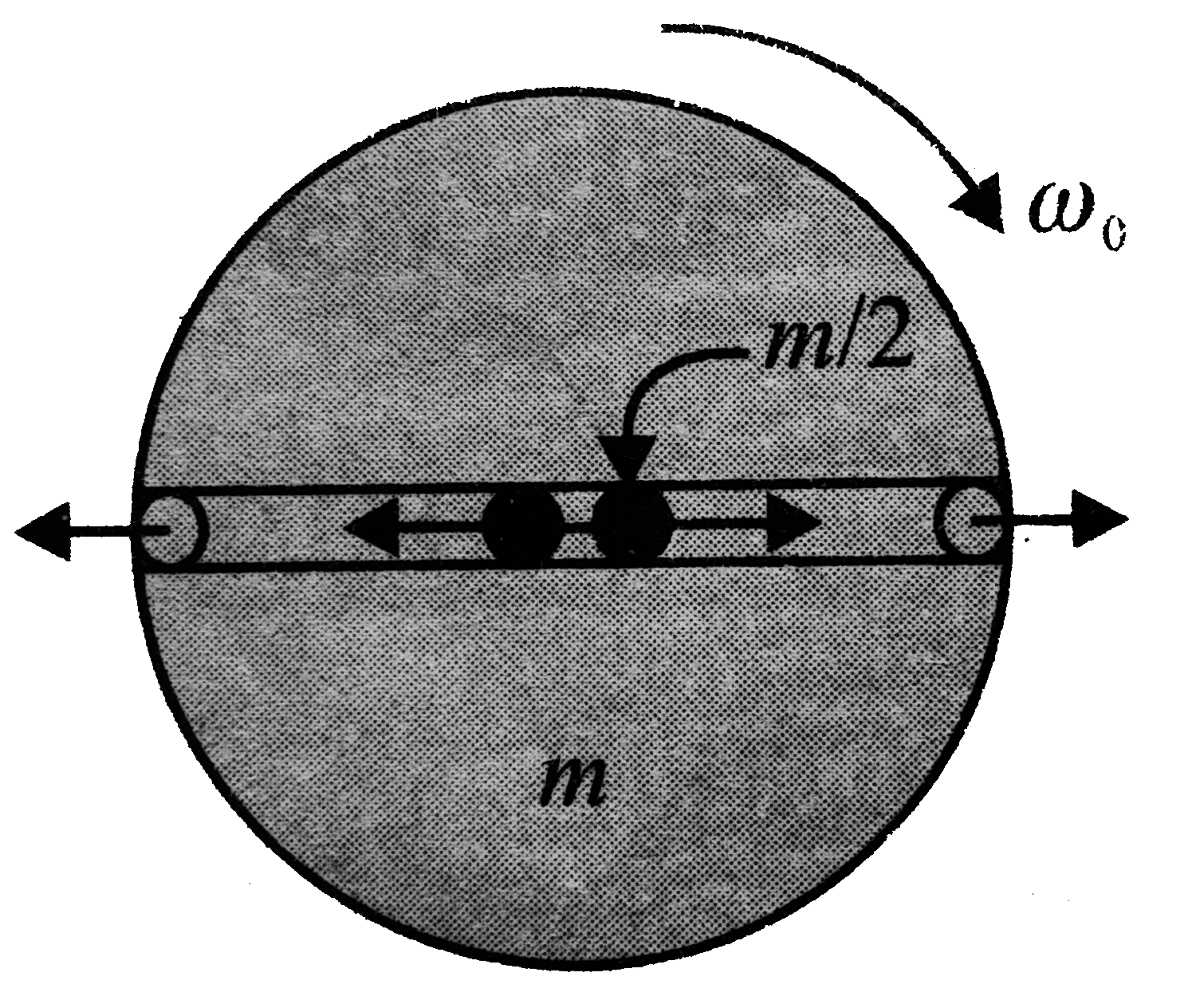
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.
The speed of each ball relative to the ground just after they leave the disc is
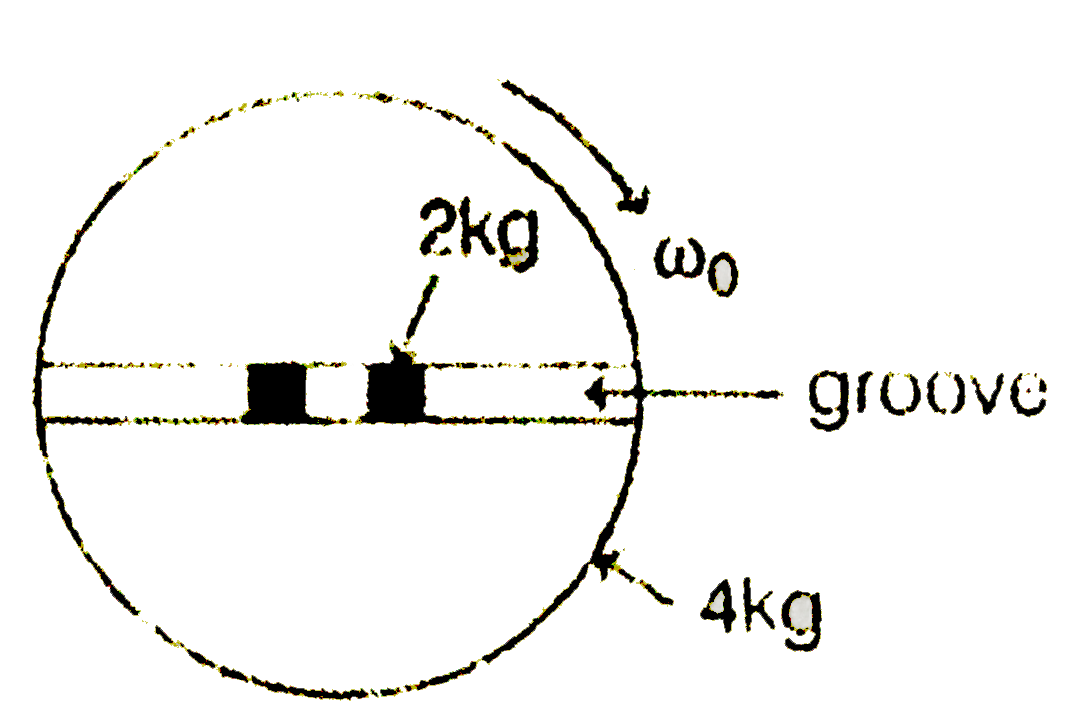
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View SolutionCircular disc of mass 2 kg and radius 1 m is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8 J. The angular momentum is (Js) is
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
View Solution
