A fireman want to slide down a rope. The breaking load the rope is 3/4th of the weight of the man. With what minimum acceleration should the fireman slide down ?
g/6
g/4
g/3
g/2
The correct Answer is:b
To solve the problem, we need to determine the minimum acceleration with which the fireman can slide down the rope without exceeding the breaking load of the rope.
1. Identify the Forces Acting on the Fireman:
- The weight of the fireman W=mg (where m is the mass of the fireman and g is the acceleration due to gravity).
- The tension in the rope T acts upwards against the weight of the fireman.
2. Set Up the Equation of Motion:
- When the fireman slides down with acceleration a, the net force acting on him can be expressed using Newton's second law:
mg−T=ma
- Rearranging gives:
T=mg−ma
3. Determine the Maximum Tension:
- According to the problem, the maximum tension Tmax that the rope can withstand is 34mg.
4. Set the Tension Equal to Maximum Tension:
- To find the minimum acceleration, we set the tension equal to the maximum tension:
mg−ma=34mg
5. Solve for Acceleration a:
- Rearranging the equation gives:
mg−34mg=ma
14mg=ma
- Dividing both sides by m (assuming m≠0):
14g=a
6. Final Result:
- Therefore, the minimum acceleration a with which the fireman should slide down is:
a=g4
- The weight of the fireman W=mg (where m is the mass of the fireman and g is the acceleration due to gravity).
- The tension in the rope T acts upwards against the weight of the fireman.
- When the fireman slides down with acceleration a, the net force acting on him can be expressed using Newton's second law:
mg−T=ma
- Rearranging gives:
T=mg−ma
- According to the problem, the maximum tension Tmax that the rope can withstand is 34mg.
- To find the minimum acceleration, we set the tension equal to the maximum tension:
mg−ma=34mg
- Rearranging the equation gives:
mg−34mg=ma
14mg=ma
- Dividing both sides by m (assuming m≠0):
14g=a
- Therefore, the minimum acceleration a with which the fireman should slide down is:
a=g4
Topper's Solved these Questions
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-2
73 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-3
49 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Example
95 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-3
34 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
Similar Questions
A monkey is decending from the branch of a tree with constant acceleration. If the breaking strength is 75% of the weight of the monkey, the minimum acceleration with which monkey can slide down without breaking the branch is
View SolutionA fireman of mass 60 kg slides down a pole. As shown in figure. He is pressing the pole with a force of 600 N. The coefficient of friction between the hands and the pole is 0.5. With wht acceleration will the fireman slide down (g=10m/s2)
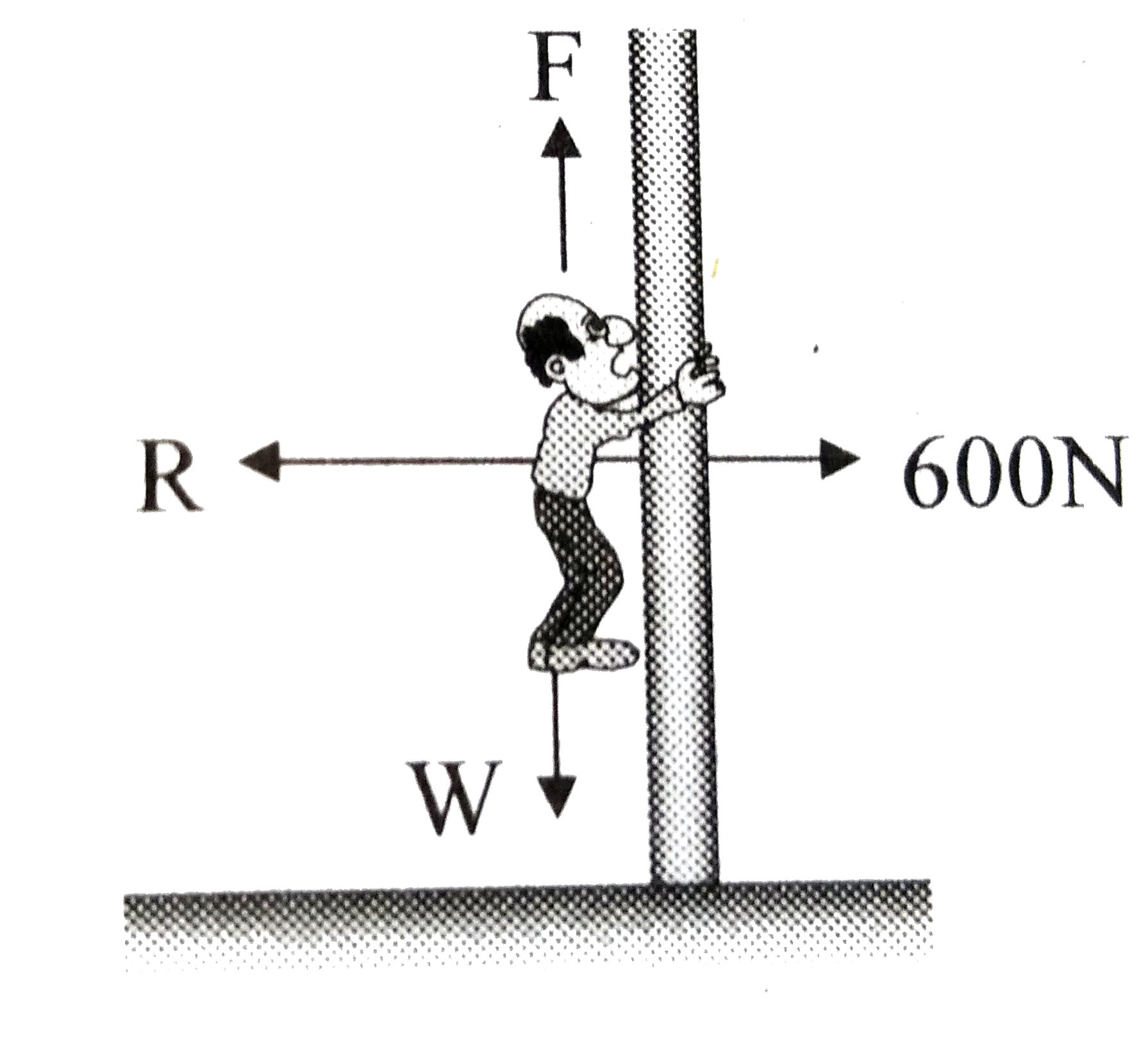
View Solution
Knowledge Check
A person wishes to slide down a rope whose breaking load is 35 of the weight of the person Minimum acceleration by which the person should slide down without breaking the rope is:
A0.8gB1.2gC0.6gD0.4gA fireman is sliding down with the help of a rope. If the breaking strength of the rope is 2mg3 where m is the mass of the man, the minimum acceleration with which the fireman can slide, so that the rope does not break, is :
Ag2Bg3Cg4D2g3A man slides down a light rope whose breaking strength is η times his weight (η<1) . What should be his minimum acceleration so that the rope just breaks?
AηgBg(1−η)Cg1+ηDg2+η
With what minimum acceleration can monkey slide down a rope whose breaking strength is two third of his weight?
View SolutionWith what minimum acceleration can a fireman slide down a rope whose breaking strength is (2/3) of his weight?
View SolutionA child weighing 25 kg slides down a rope hanging from the branch of a tall tree. If the force of friction acting against him is 2 N , what is the acceleration of the child
View SolutionA man slides down a light rope whose breaking strength in η times his weight (η<1). What should be his maximum acceleration so that the rope just breaks ?
View SolutionA fireman of mass 60 kg slides down a pole. He is pressing the pole with a force of 600N. The coefficient of friction between the hands and the pole is 0.5, with what acceleration will the fireman slide down (g=10ms2)
View Solution