A block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
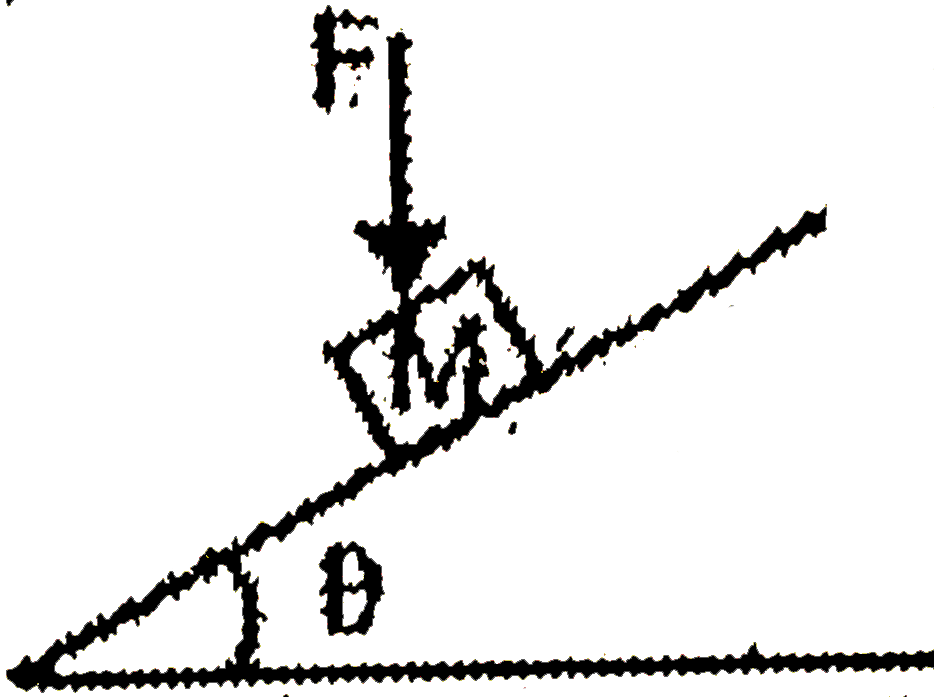
(F+Mg)sinθ
μk(F+Mg)cosθ
μsMgcosθ
(Mg+F)sinθ
The correct Answer is:b
Step by step video, text & image solution for A block of mass M is sliding down the plane. Coefficient of static friction is mu_(s) and kinetic friction is mu_(k). Then friction force acting on the block is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-273videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-349videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Example95videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-334videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
Similar Questions
In Fig. 6-29, a force →P acts on a block weighing 45 N. The block is initially at rest on a plane inclined at angle θ=15∘ to the horizontal. The positive direction of the r axis is up the plane. Between block and plane, the coefficient of static friction is μs=0.50 and the coefficient of kinetic friction is μk=0.34. In unitvector notation, what is the frictional force on the block from the plane when →P is (a)(−5.0N)ˆi,(b)(−8.0N)ˆi,and(c)(−15N)ˆi?
 View Solution
View SolutionA block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).View Solution
Knowledge Check
- Question 1 - Select One
If coefficient of static friction is μs and coefficient of kinetic friction is μk , which one is correct ?
Aμs=μkBμs>μkCμs<μkDμs≤μk - Question 2 - Select One
The ratio of μk (kinetic friction) and μs (state friction) is
Agreater than 1Bless than 1Cequal to 1Ddepends on condition - Question 3 - Select One
A force of 100N is applied on a block of mass 3kg as shown in the figure. The coefficient of friction between the surface and the block is μ=1√3 . The friction force acting on the bock is.
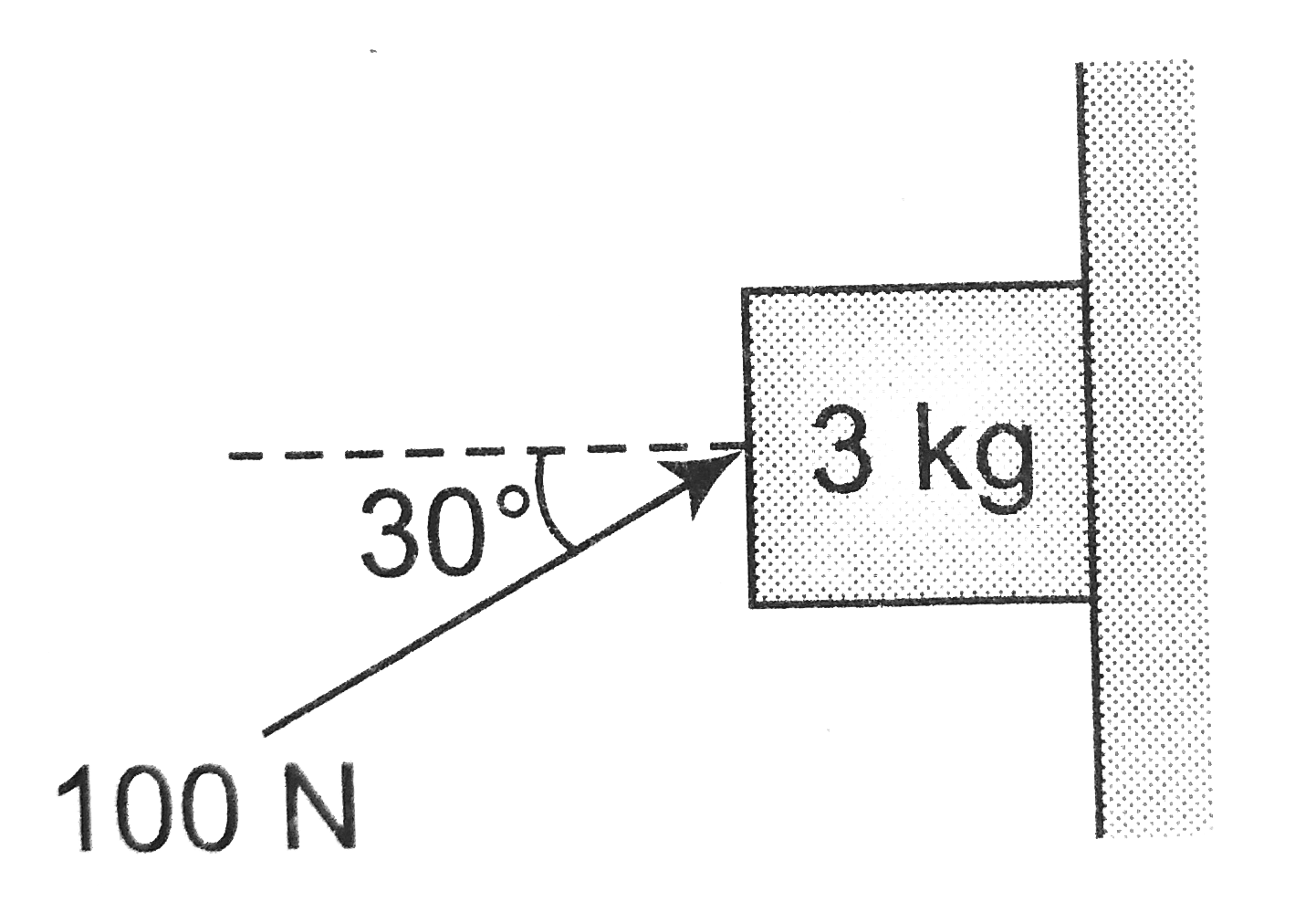 A15N downwardB25N upwardC20N downwordD30N upward
A15N downwardB25N upwardC20N downwordD30N upward
In the arrangement shown in the figure, friction exists only between the two blocks, A and B. The coefficient of static friction μs=0.6 and coefficient of kinetic friction μk=0.4, the masses of the blocks A and B are m1=20kg and m2=30kg, respectively. Find the acceleration (in ms−2) of m1, if a force F=150N is applied, as shown in the figure. [Assume that string and pulleys are massless]
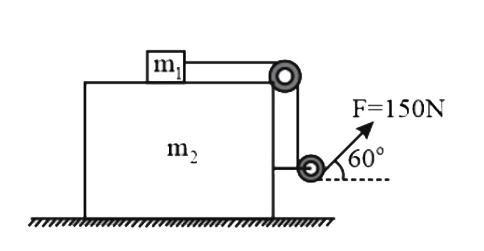 View Solution
View SolutionA block of mass 20 kg is pushed with a horizontal force of 90N. If the coefficient of static and kinetic friction are 0.4 and 0.3, the frictional force acting on the block is (g=10ms−2)
View SolutionA block of mass 20kg is pushed with a horizontal force of 90N. It the coefficient of static and kinetic friction are 0.4 and 0.3, the frictional force acting on the block is (g=10ms−2) .
View SolutionWhich is true for rolling friction (μr), static friction (μs) and kinetic friction (μk) ?
View SolutionIf coefficient of friction between both the block is μ−12 . Find friction force acting between both block.
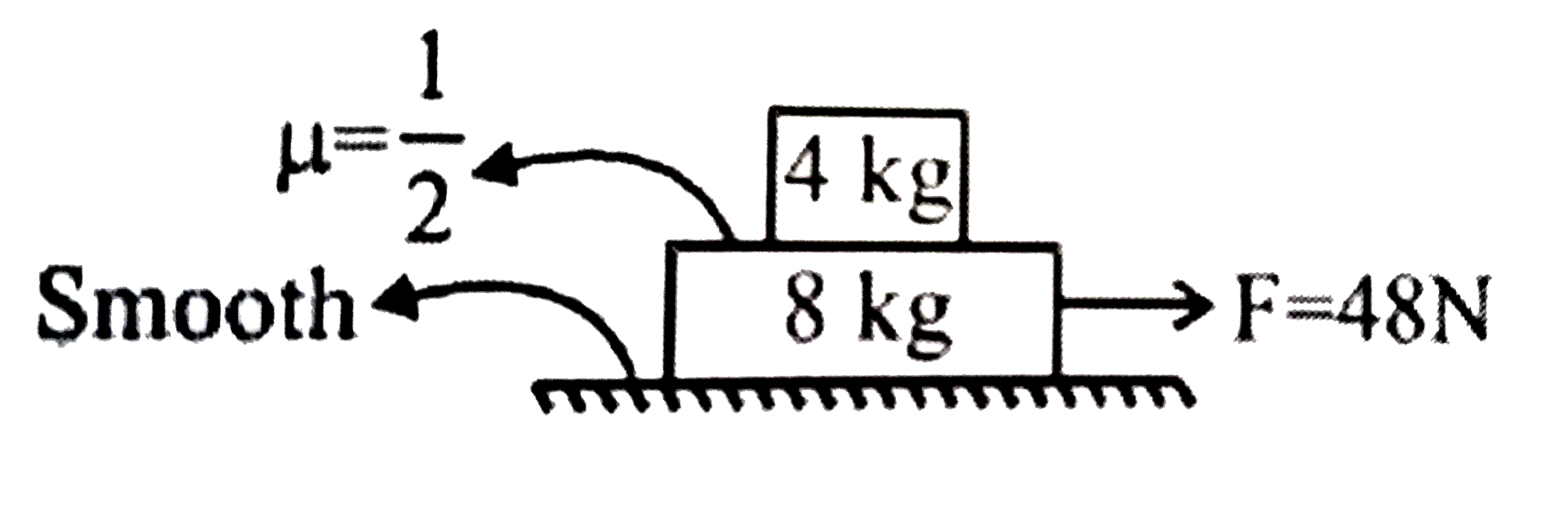 View Solution
View Solution

