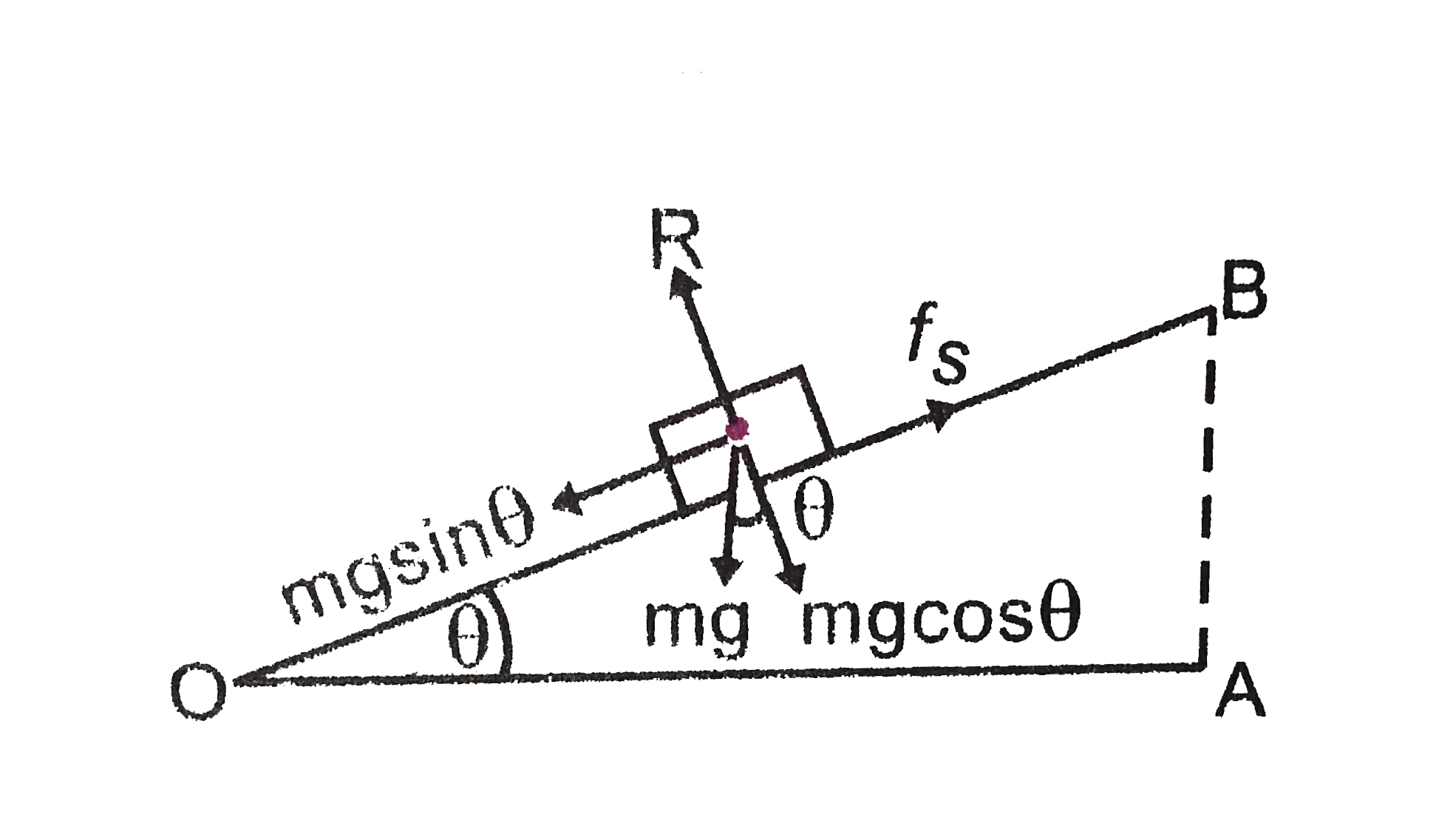
In Fig. 6-29, a force →P acts on a block weighing 45 N. The block is initially at rest on a plane inclined at angle θ=15∘ to the horizontal. The positive direction of the r axis is up the plane. Between block and plane, the coefficient of static friction is μs=0.50 and the coefficient of kinetic friction is μk=0.34. In unitvector notation, what is the frictional force on the block from the plane when →P is (a)(−5.0N)ˆi,(b)(−8.0N)ˆi,and(c)(−15N)ˆi?

→fs=(17N)ˆi,(b)→fs=(20N)ˆi,(c)→fk=(15N)ˆi
Topper's Solved these Questions
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
23 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
4 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - CHECKPOINTS
5 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
3 Videos
Similar Questions
Coefficient of kinetic friction and coefficient of static friction between two blocks is μk and μs respectively. In general
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View Solution
Knowledge Check
A block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
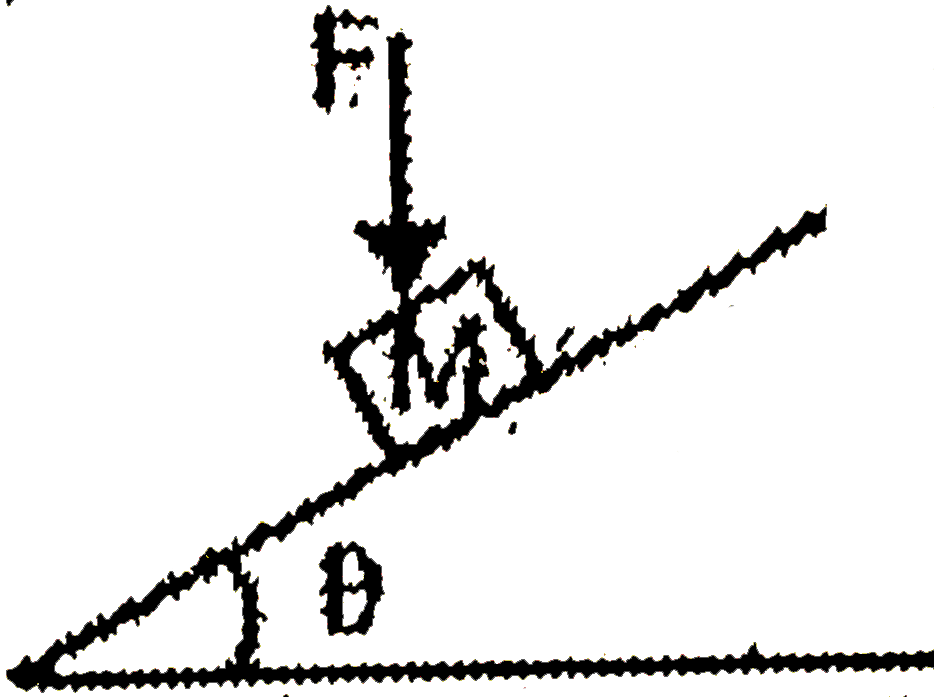 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
AmgBμmgcosθCmgsinθDμmgtanθA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8N
A block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionThe coefficient of friction between the block and the inclined plane is μ.
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
View Solution
