A particle is moving on a straight line. It is initially at rest
v= instantaneous velocity
P = instantaneous power S = displacement
F= force t = time
Match the possible expression of the quantities in column-1 with the situation in column-2
Column-1Column-2(A)v3∝S(P)P = constant(B)v2∝t(Q)P∝v(C)v2∝S(R)F = constant(D)v∝t(S)F∝1v(T)P∝t
The correct Answer is:A-P, S; B-P, S; C-R, T; D-Q, R, T
Topper's Solved these Questions
Similar Questions
In the diagram shown in figure mass of both the balls in same. Match the following columns.
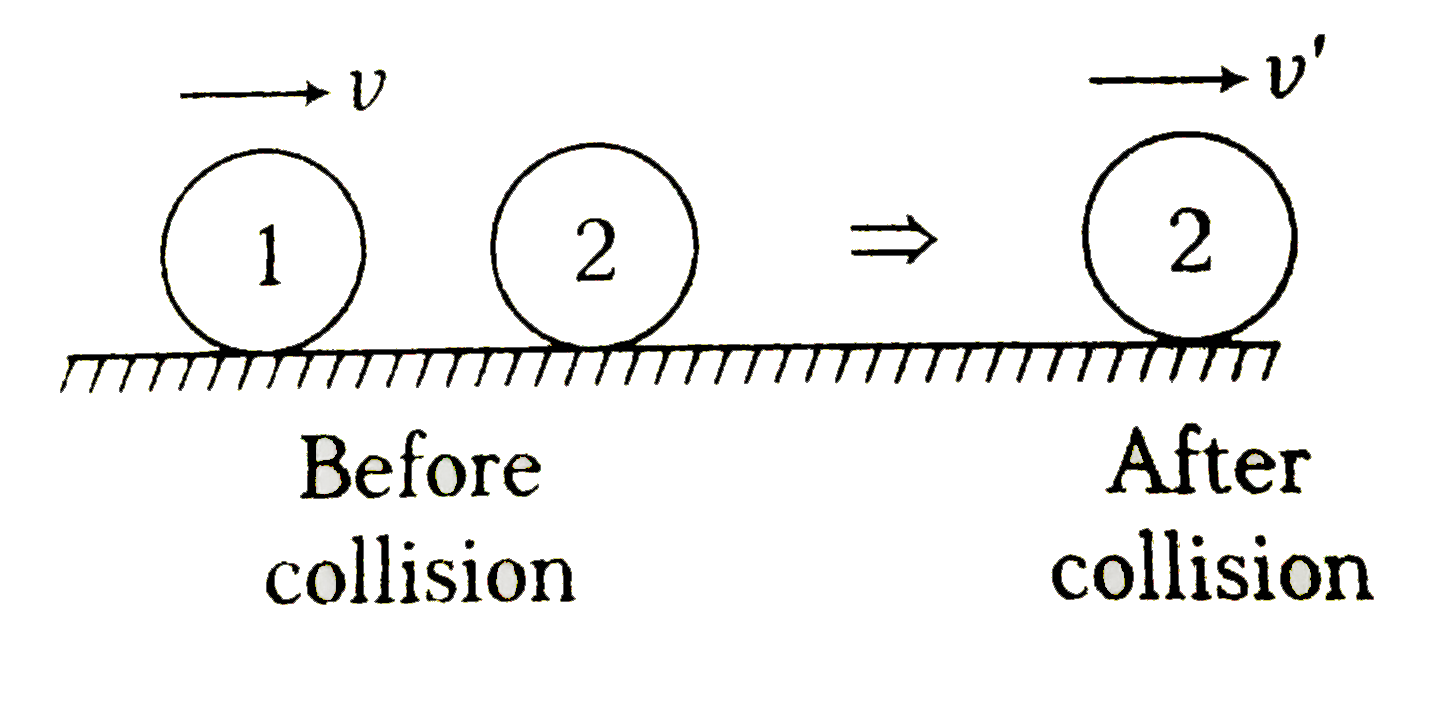
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficient
View SolutionIn the diagram shown in figure mass of both the balls in same. Match the following columns.
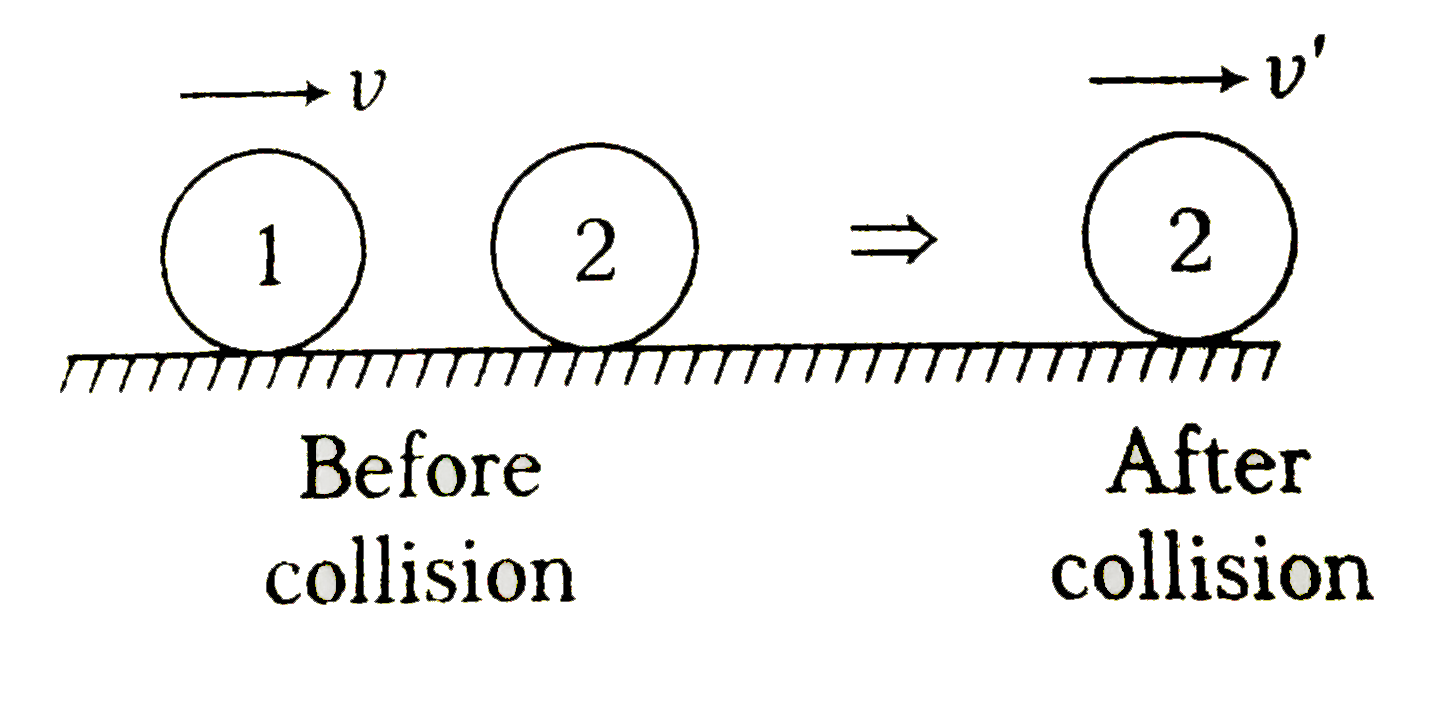
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficient
View Solution
Knowledge Check
The velocity v varies as v=α√x,where x represents the displacement. At t=0 it is located x=0 Then x∝
At3BtCt1/2Dt2A particle moves in a circular path such that its speed v varies with distance s as v=α√s, where α is a positive constant. Find the acceleration of the particle after traversing a distance s.
Aα√14+s2R2Bα2√14+sRCα√14+sRDα2√14+s2R2
A body is moved along a straight line by a machine delivering a power proportional to time (P∝t) Then match the following :
Column-1 Column-2(A)Velocity is proportional to(P) t(B)Displacement proportional to(Q)t2(C)Work done proportional to(R)t3
View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
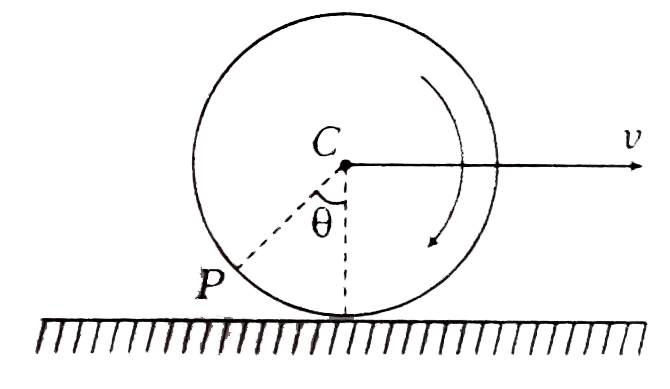
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns

Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View SolutionA particle is moving in a straight line such that dv/dt=−λv, where v is the velocity and λ is a constant. At t=0, the particle is at the origin and moves with velocity v0. Sketch the following graphs:
(a)v−t(b)s−t(c)v−s(d)logevv/st
View SolutionMatch the Column-I with Column-II :
Column-IColumn-II(a)First order(p)Unit ofk=sec−1(b)Pseudo first order(q)Unit ofk=dm6mol−2s−1(c)Third order(r)t1/2∝1/a2(d)Second order(s)t1/2∝1a
View SolutionA particle moves in a circular path such that its speed 1v varies with distance s as v=√s, where ∝ is a positive constant. Find the acceleration of the particle after traversing a distance s.
View Solution
