A disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
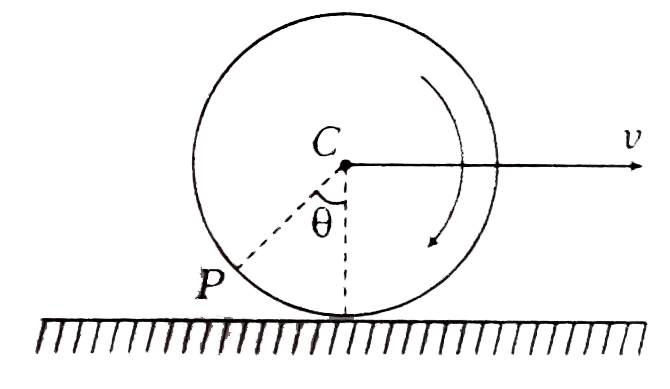
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
The correct Answer is:(A→q,B→p,C→s,D→r)
In gerenal as vP=2vsin(θ2)
If θ=90∘, then vP=2vsin(60∘2)=2v×12=v
⇒(A)→(q)
If θ=90∘, then vP=2vsin(90∘2)=2v×1√2=√2v
⇒(B)→(p)
If θ=120∘, then vP=2vsin(120∘2)=2v×√32=√3v
⇒(C)→(s)
If θ=180∘, then vP=2vsin(180∘2)=2v⇒(D)→(r).
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A disc rolls on ground without slipping . Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ . Suppose vp is the speed of this point. Then, match the following the following table.

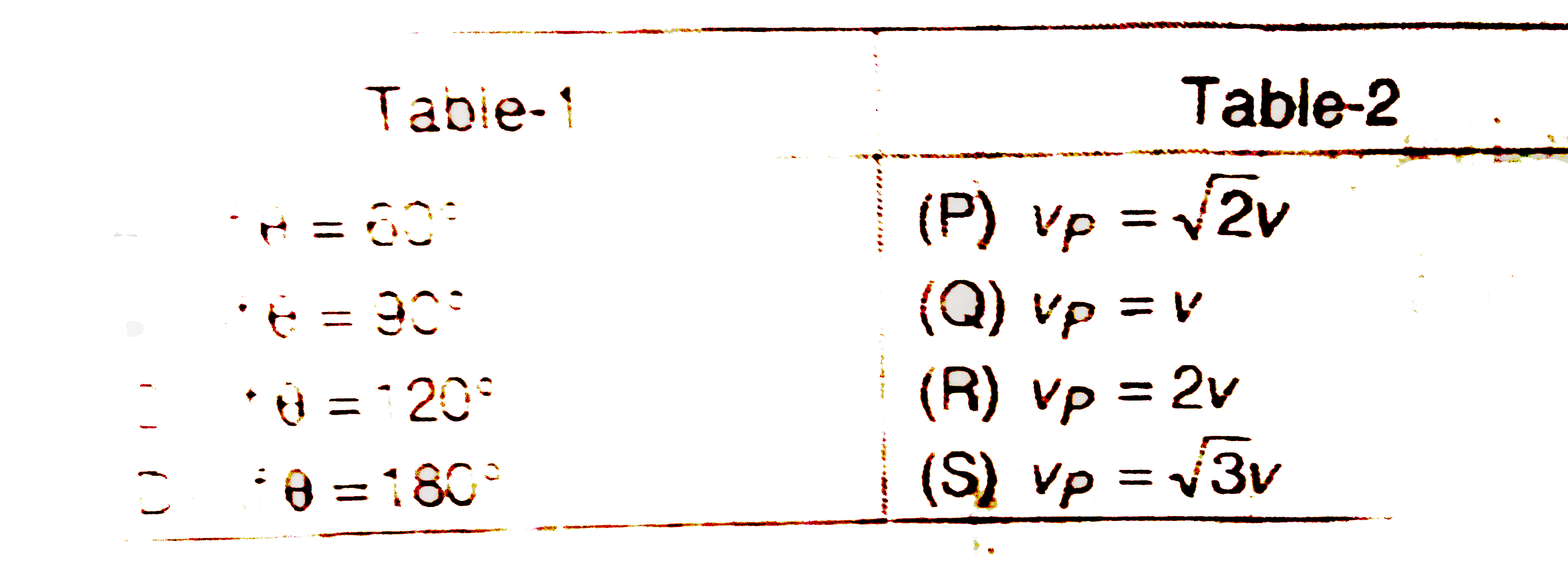
View SolutionA disc rolls on ground without slipping . Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ . Suppose vp is the speed of this point. Then, match the following the following table.


View Solution
Knowledge Check
A hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
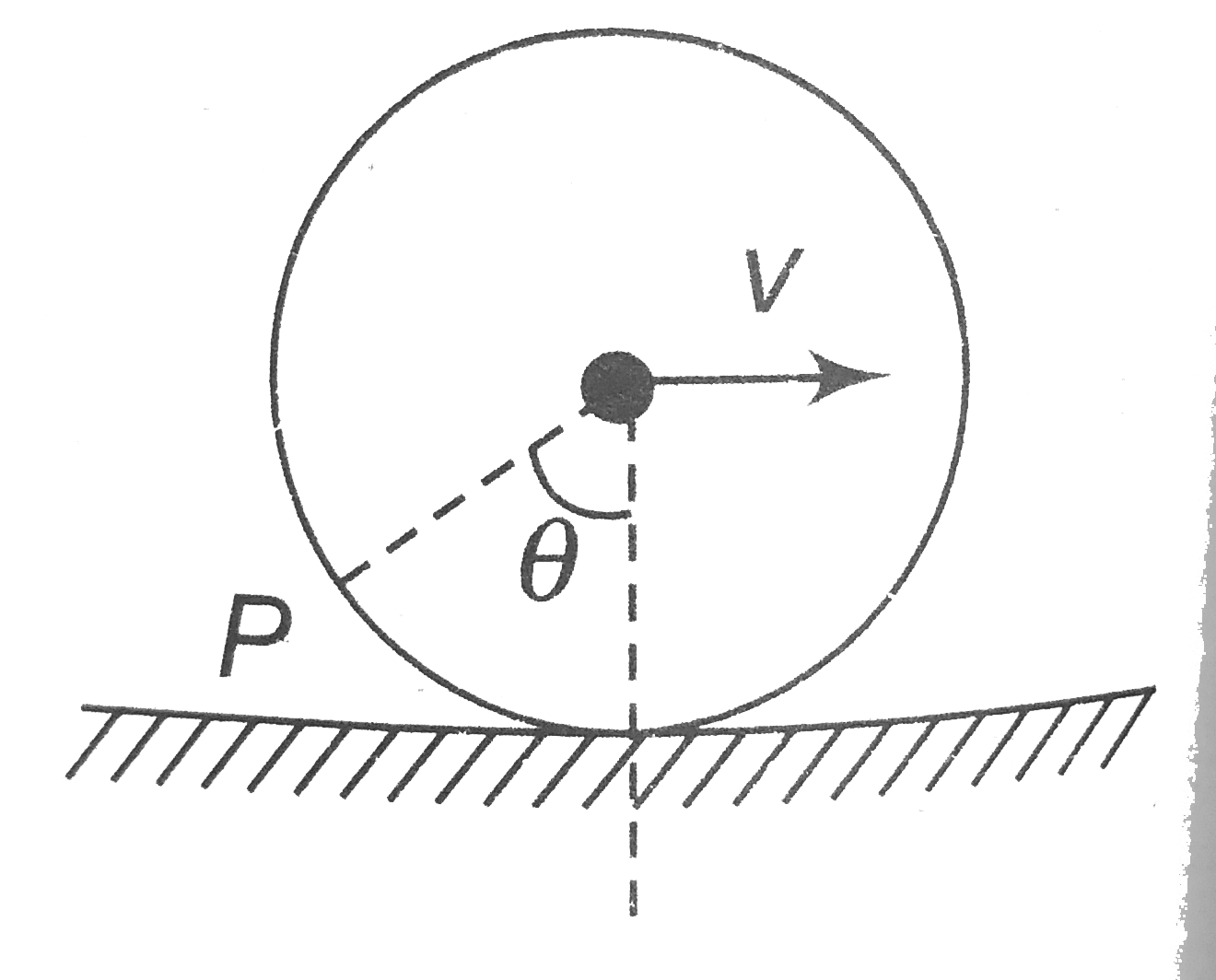 A2vsin(θ/2)BvsinθC2vcos(θ/2)Dvcosθ
A2vsin(θ/2)BvsinθC2vcos(θ/2)DvcosθA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.
 AVB2VC3VD2V3
AVB2VC3VD2V3A disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is
 A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆj
A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆj
A hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :

View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.

View SolutionA wheel is rolling straight on ground without slipping. If the axis of the wheel has speed v, the instantenous velocity of a point P on the rim, defined by angle θ, relative to the ground will be

View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionIn the diagram shown in figure mass of both the balls in same. Match the following columns.
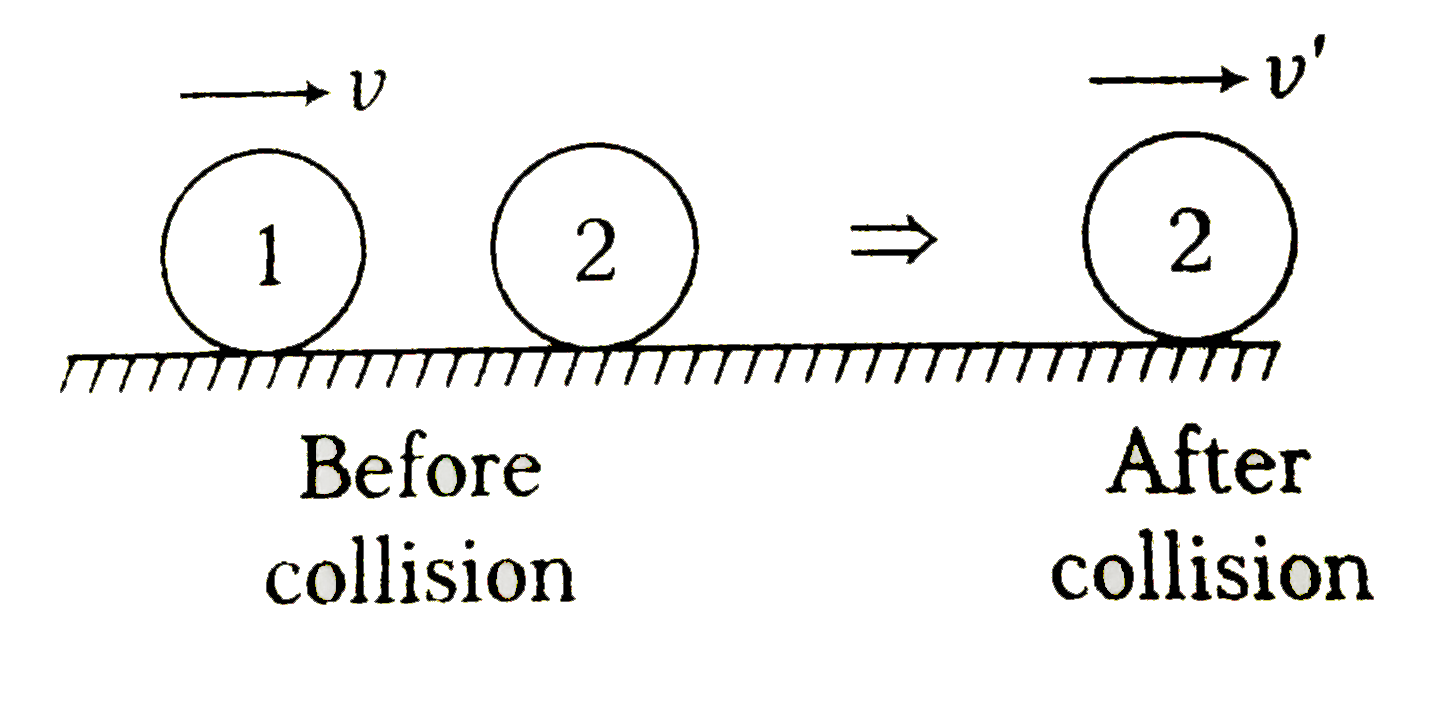
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficient
View Solution
