In the figure above, the bases , ABC and DEF, of the right prism are equilateral triangles. The altitude of the prism is BE. If a plane cuts the figure through points A, C and E, two solids, EABC, and EACFD, are formed. What is the ratio of the volume of EABC to the volume of EACFD?
14
13
√34
12
The correct Answer is:D
The volume of the prism is area of base times height. The figure EABC is a pyramid with base triangle ABC and height BE, the same as the base the height of the prism. The volume of the pyramid is 13(base times height),13 the volume of the prism. Therefore, the other solid EACFD, is 23 the volume of the prism. The ratio of the volume is 12. [15]
Topper's Solved these Questions
Similar Questions
Knowledge Check
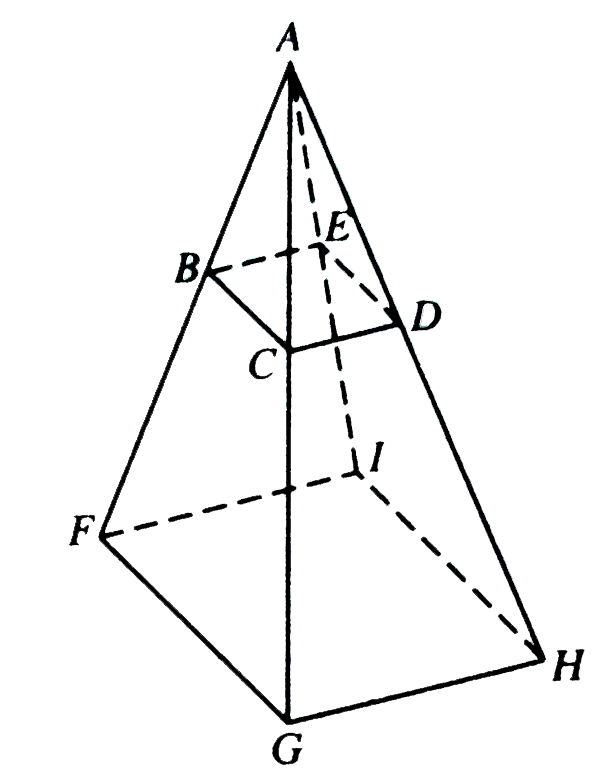
The pyramid in the figure above has square base FGHI , and all triangular faces are congruent. The base BCDE of the small pyramid is also square , and is parallel to FGHI. If the ratio of the area of square BCDE to the area of square FGHI is 1:4 , what is the ratio of the volume of the small pyramid to the volume of the large pyramid ?A1:2B1:3C1:4D1:8
The figure above shows a logo in the shape of overlapping equilateral triangles ABC and DEF. if AD=DC=CF=4, what is the area of the shaded region?A24√3−8B4√3C32√3D36√3−8
A solid cone of base radius 10 cm is cut into two parts through the mid-point of its height, by a plane parallel to its base. Find the ratio in the volumes of two parts of the cone.
View SolutionA solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is:
View SolutionA cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base Find the ratio of the volumes of two parts
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC in F. Prove that: ar(△BFE)=2ar(△FED).
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC. If AE intersects BC in F, Prove that: ar(BDE)=14ar ( ABC).
View SolutionThe position vectors of the vertices A, B and C of a tetrahedron ABCD are ˆi+ˆj+ˆk, ˆk, ˆi and ˆ3i,respectively. The altitude from vertex D to the opposite face ABC meets the median line through Aof triangle ABC at a point E. If the length of the side AD is 4 and the volume of the tetrahedron is2√2/3, find the position vectors of the point E for all its possible positions
View Solution