Doubtnut Promotions Sticky

16-18 The graph of polynomial function f is shown above. Q. What is the maximum number of points a circle whose center is at the origin can intersect the graph of y=f(x)?
16-18 The graph of polynomial function f is shown above.
Q. What is the maximum number of points a circle whose center is at the origin can intersect the graph of y=f(x)?

A

2

B

3

C

4

D

6

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

|
Answer

Step by step video, text & image solution for 16-18 The graph of polynomial function f is shown above. Q. What is the maximum number of points a circle whose center is at the origin can intersect the graph of y=f(x)? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSPASSPORT TO ADVANCED MATH

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    ocr_image
    16-18 The graph of polynomial function f is shown above.
    Q. What is the best estimate of the remainder when f(x) is divided by x+3?

    A−6.0
    B0
    C6.5
    DIt cannot be determined.
  • Question 2 - Select One

    ocr_image
    16-18 The graph of polynomial function f is shown above.
    Q.What is the greatest integer value of k for which f(x)=k has exactly 3 real solutions?

    A−5
    B0
    C6
    D7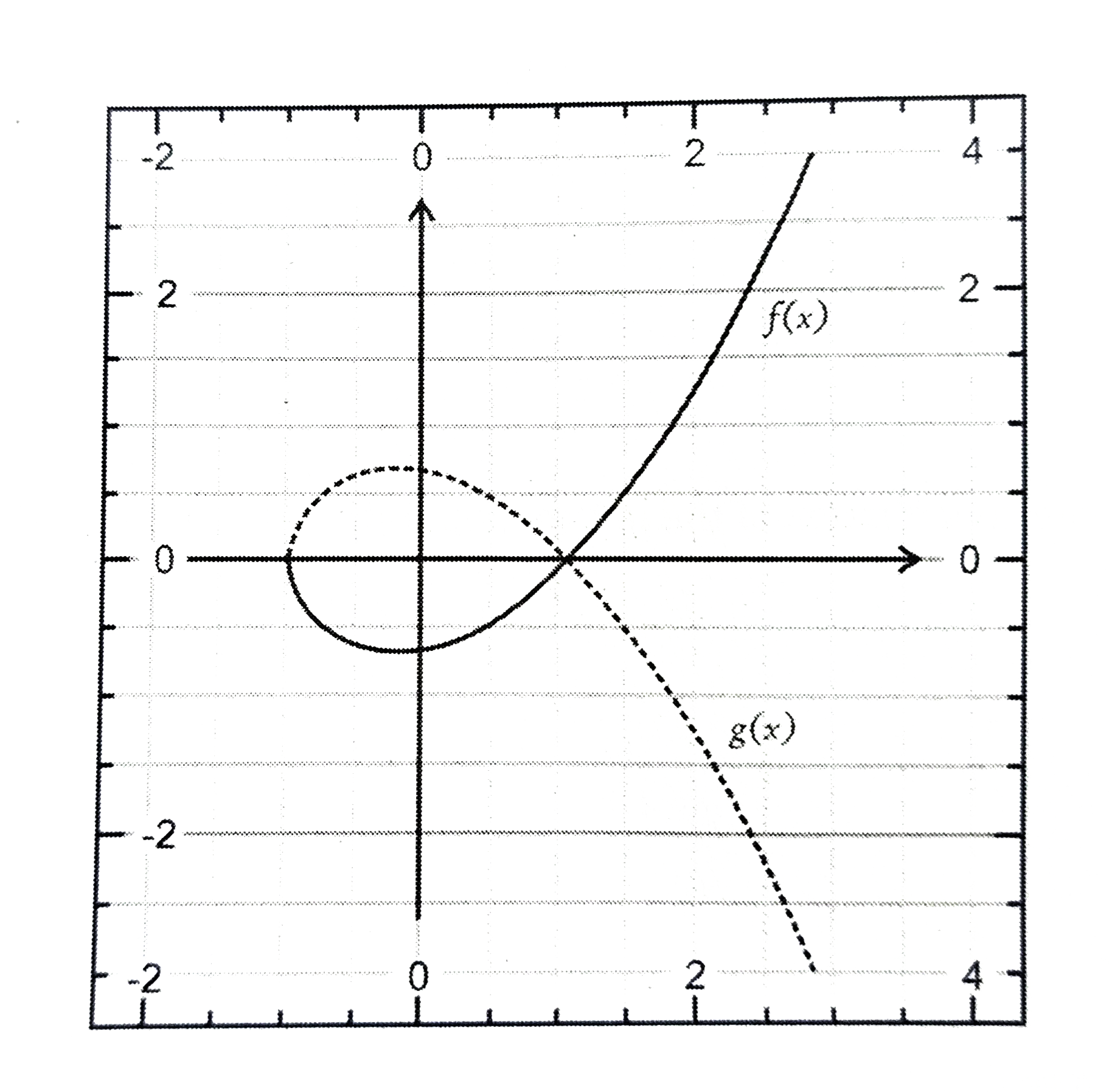
  • Question 3 - Select One

    ocr_image
    The graph of f(x) and g(x) are shown above . Which options is true ?

    Af(x)=g(−x)
    Bf(x)=g(x)−x
    Cf(x)=−g(x)
    Df(x)=−g(−x)