The endpoints of ¯¯¯¯¯¯AB are A(0, 0) and B(9, -6). What is an equation of the line that contains the reflection of ¯¯¯¯¯¯AB in the y-axis?
y=−32x
y=−23x
y=−x+3
y=23x
The correct Answer is:D
To find the equation of the line that contains the reflection of the line segment ¯¯¯¯¯¯¯¯AB in the y-axis, we will follow these steps:
Step 1: Identify the endpoints of the line segment ¯¯¯¯¯¯¯¯AB
The endpoints are given as A(0,0) and B(9,−6).
Step 2: Calculate the slope of the line segment ¯¯¯¯¯¯¯¯AB
The formula for the slope m of a line through two points (x1,y1) and (x2,y2) is:
m=y2−y1x2−x1
Here, (x1,y1)=(0,0) and (x2,y2)=(9,−6).
Substituting the values:
m=−6−09−0=−69=−23
Step 3: Determine the slope of the reflected line
When a line is reflected across the y-axis, the slope of the reflected line is the negative of the original slope. Therefore, the slope of the reflected line will be:
mreflected=−(−23)=23
Step 4: Use the point-slope form to find the equation of the reflected line
The point-slope form of a line is given by:
y−y1=m(x−x1)
We can use point A(0,0) for the reflected line. Substituting m=23, x1=0, and y1=0:
y−0=23(x−0)
This simplifies to:
y=23x
Conclusion
The equation of the line that contains the reflection of ¯¯¯¯¯¯¯¯AB in the y-axis is:
y=23x
The endpoints are given as A(0,0) and B(9,−6).
The formula for the slope m of a line through two points (x1,y1) and (x2,y2) is:
m=y2−y1x2−x1
Here, (x1,y1)=(0,0) and (x2,y2)=(9,−6).
m=−6−09−0=−69=−23
When a line is reflected across the y-axis, the slope of the reflected line is the negative of the original slope. Therefore, the slope of the reflected line will be:
mreflected=−(−23)=23
The point-slope form of a line is given by:
y−y1=m(x−x1)
We can use point A(0,0) for the reflected line. Substituting m=23, x1=0, and y1=0:
y−0=23(x−0)
This simplifies to:
y=23x
The equation of the line that contains the reflection of ¯¯¯¯¯¯¯¯AB in the y-axis is:
y=23x
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - PASSPORT TO ADVANCED MATHEXERCISE - Grib-In29videos
PASSPORT TO ADVANCED MATH
- BOOK - ENGLISH SATCHAPTER - PASSPORT TO ADVANCED MATHEXERCISE - EXERCISE80videos
PASSPORT TO ADVANCED MATH
- BOOK - ENGLISH SATCHAPTER - PASSPORT TO ADVANCED MATHEXERCISE - EXERCISE80videos
PASSPORT TO ADVANCED MATH
- BOOK - ENGLISH SATCHAPTER - PARAMETRIC EQUATIONS EXERCISE - EXERCISES3videos
PARAMETRIC EQUATIONS
- BOOK - ENGLISH SATCHAPTER - PIECEWISE FUNCTIONSEXERCISE - EXERCISES8videos
PIECEWISE FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
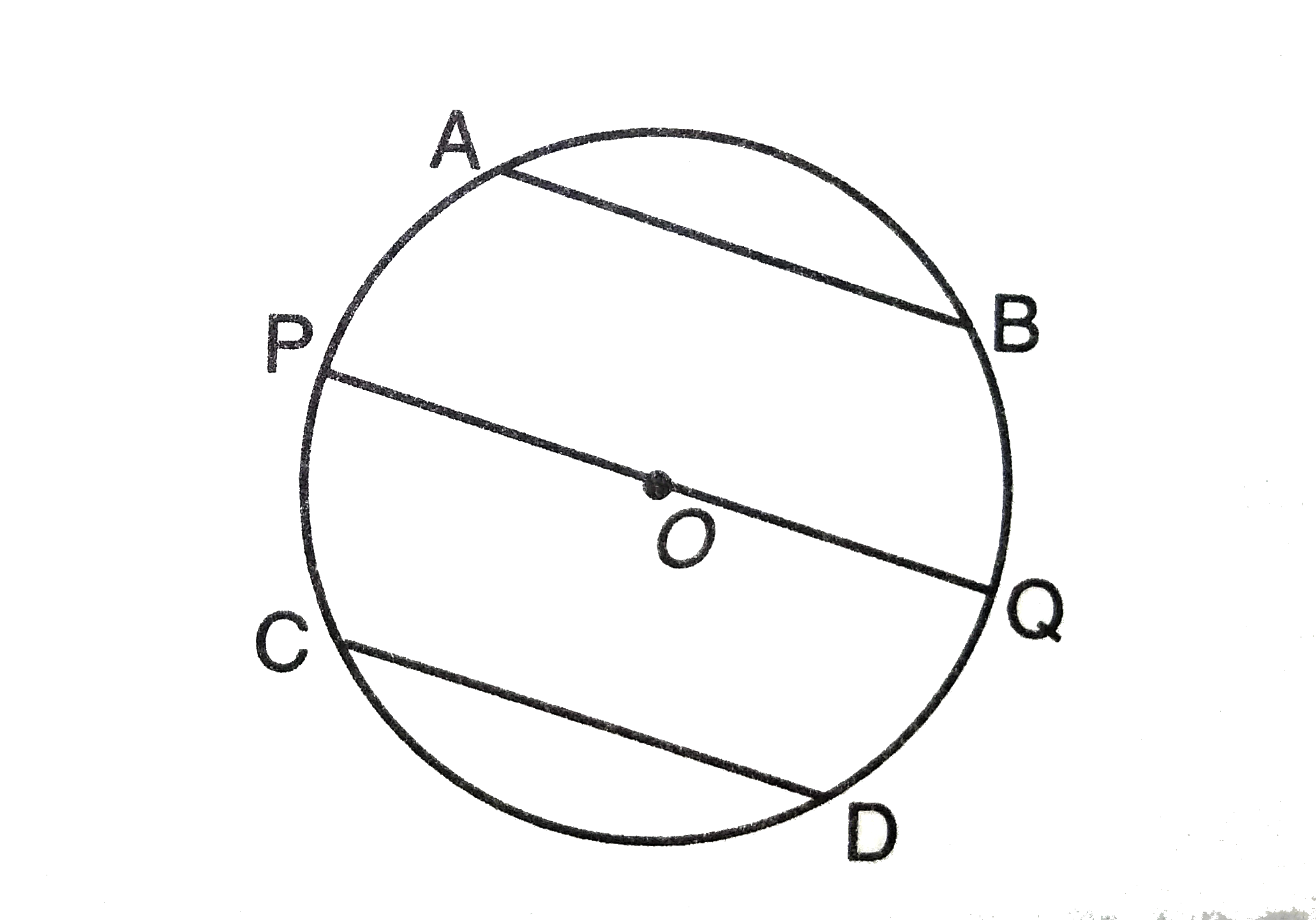
In the figure above, ¯¯¯¯¯¯PQ is a diameter of circle O, ¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯PQ∣∣∣∣¯¯¯¯¯¯CD,and¯¯¯¯¯¯AB=¯¯¯¯¯¯CD. The length of chord ¯¯¯¯¯¯AB is 34 of the length of diameter ¯¯¯¯¯¯PQ. If r represents the radius length of circle O, what is the distance between chords ¯¯¯¯¯¯ABand¯¯¯¯¯¯CD in terms r?A54rB√74rC32rD√72r
The points A, B and Care (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC.
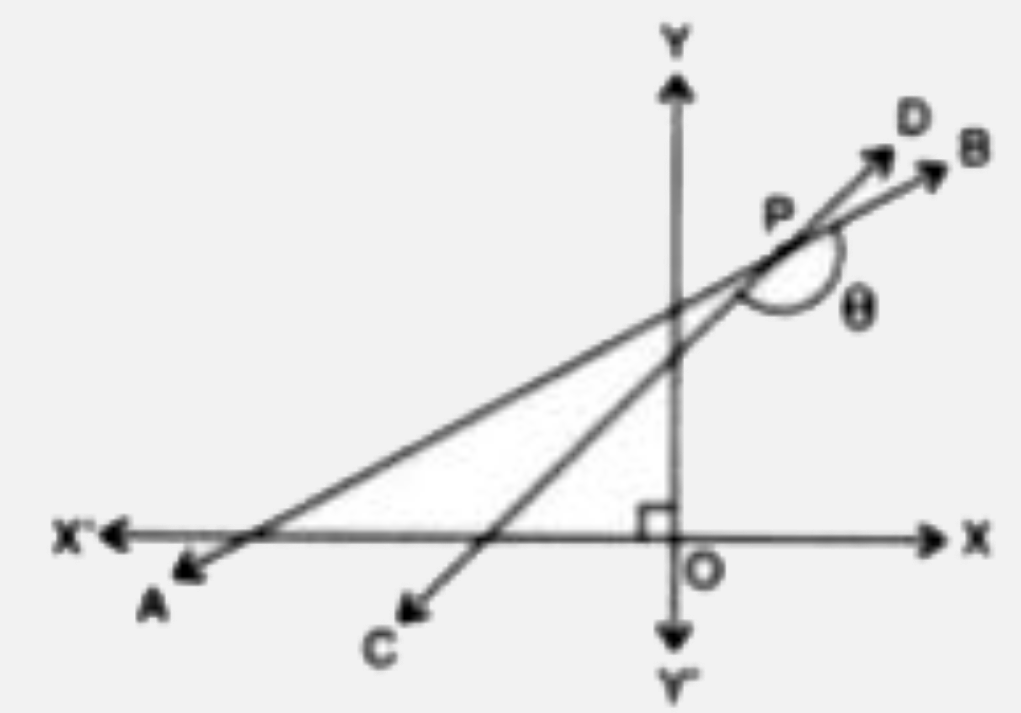
If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.View SolutionThe drawn alongiside (not drawn to scale) shows two stragit lines AB and CD. If the equation of line AB is: x−√3y+5=0 and the equation of line CD is : x−y=2, write down the inclinations of lines AB and CD, also find the angle θ i.e., angle CPB.
 View Solution
View SolutionIn the accomapanying figure, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. If AB=40,CD=16,andBC=49, what is the length of ¯¯¯¯¯¯BE?
 View Solution
View SolutionThe equation of the line AB is y=x. If A and B lie on the same side of the line mirror 2x−y=1, then the equation of the image of AB is
View Solution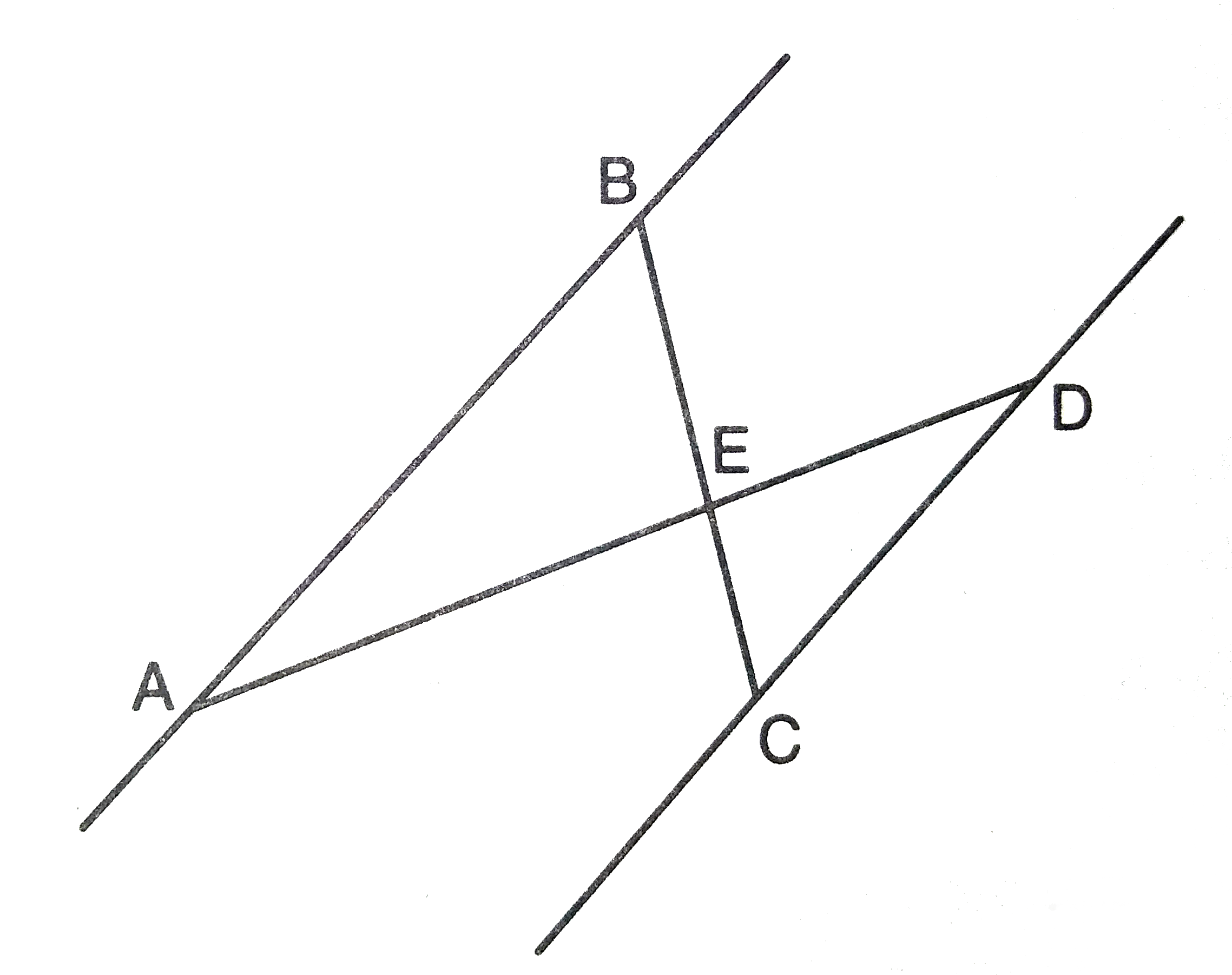
In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD, AD=30, AB=21, and CD=15. What is the length of ¯¯¯¯¯¯DE?View SolutionOn the xy plane where O is the origin, given points, A(1,0),B(0,1)andC(1,1). Let P,Q,andR be moving points on the line OA,OB,OC respectively such that ¯¯¯¯¯¯OP=45t¯¯¯¯¯¯¯¯¯(OA),¯¯¯¯¯¯OQ=60t¯¯¯¯¯¯¯¯¯(OB),¯¯¯¯¯¯OR=(1−t)¯¯¯¯¯¯¯¯¯(OC) with t>0. If the three points P,QandR are collinear then the value of t is equal to
A 1106
B 7187
C 1100
D none of theseView SolutionThe equation of a line AB is 2x−2y+3=0.
Calculate the angle that the line AB makes with the positive direction of the x-axis.View Solution

