On the xy plane where O is the origin, given points, A(1,0),B(0,1)andC(1,1). Let P,Q,andR be moving points on the line OA,OB,OC respectively such that ¯¯¯¯¯¯OP=45t¯¯¯¯¯¯¯¯¯(OA),¯¯¯¯¯¯OQ=60t¯¯¯¯¯¯¯¯¯(OB),¯¯¯¯¯¯OR=(1−t)¯¯¯¯¯¯¯¯¯(OC) with t>0. If the three points P,QandR are collinear then the value of t is equal to
A 1106
B 7187
C 1100
D none of these
1106
7187
1100
none of these
The correct Answer is:B
To solve the problem, we need to find the value of t such that the points P,Q, and R are collinear. Let's break down the solution step by step.
Step 1: Define the position vectors
Given the points:
- A(1,0)
- B(0,1)
- C(1,1)
The position vectors of these points are:
- ¯¯¯¯¯¯¯¯OA=^i
- ¯¯¯¯¯¯¯¯OB=^j
- ¯¯¯¯¯¯¯¯OC=^i+^j
Step 2: Express the position vectors of points P,Q, and R
The position vectors of points P,Q, and R are given as:
- ¯¯¯¯¯¯¯¯OP=45t⋅¯¯¯¯¯¯¯¯OA=45t^i
- ¯¯¯¯¯¯¯¯¯OQ=60t⋅¯¯¯¯¯¯¯¯OB=60t^j
- ¯¯¯¯¯¯¯¯OR=(1−t)⋅¯¯¯¯¯¯¯¯OC=(1−t)(^i+^j)=(1−t)^i+(1−t)^j
Step 3: Write the vectors ¯¯¯¯¯¯¯¯PR and ¯¯¯¯¯¯¯¯¯RQ
We need to find the vectors ¯¯¯¯¯¯¯¯PR and ¯¯¯¯¯¯¯¯¯RQ:
- ¯¯¯¯¯¯¯¯PR=¯¯¯¯¯¯¯¯OR−¯¯¯¯¯¯¯¯OP=((1−t)^i+(1−t)^j)−(45t^i)=(1−t−45t)^i+(1−t)^j=(1−46t)^i+(1−t)^j
- ¯¯¯¯¯¯¯¯¯RQ=¯¯¯¯¯¯¯¯¯OQ−¯¯¯¯¯¯¯¯OR=(60t^j)−((1−t)^i+(1−t)^j)=−(1−t)^i+(60t−(1−t))^j=−(1−t)^i+(61t−1)^j
Step 4: Set up the condition for collinearity
For points P,Q,R to be collinear, the vectors ¯¯¯¯¯¯¯¯PR and ¯¯¯¯¯¯¯¯¯RQ must be parallel. This means there exists a scalar λ such that:
¯¯¯¯¯¯¯¯PR=λ¯¯¯¯¯¯¯¯¯RQ
Step 5: Equate the components
From the vectors we derived:
1. 1−46t=−λ(1−t) (i-component)
2. 1−t=λ(61t−1) (j-component)
Step 6: Solve the equations
From the first equation:
λ=−1−46t1−t
Substituting λ into the second equation:
1−t=−1−46t1−t(61t−1)
Cross-multiplying gives:
(1−t)(1−t)=−(1−46t)(61t−1)
Expanding both sides:
(1−2t+t2)=−(61t−1+46t2−46t)
1−2t+t2=−61t+1+46t2
Rearranging gives:
0=45t2−59t
Factoring out t:
t(45t−59)=0
Thus, t=0 or t=5945.
Step 7: Check if t is valid
Since t>0, we have:
t=5945
Conclusion
The value of t that makes points P,Q,R collinear is t=7187.
Given the points:
- A(1,0)
- B(0,1)
- C(1,1)
- ¯¯¯¯¯¯¯¯OA=^i
- ¯¯¯¯¯¯¯¯OB=^j
- ¯¯¯¯¯¯¯¯OC=^i+^j
The position vectors of points P,Q, and R are given as:
- ¯¯¯¯¯¯¯¯OP=45t⋅¯¯¯¯¯¯¯¯OA=45t^i
- ¯¯¯¯¯¯¯¯¯OQ=60t⋅¯¯¯¯¯¯¯¯OB=60t^j
- ¯¯¯¯¯¯¯¯OR=(1−t)⋅¯¯¯¯¯¯¯¯OC=(1−t)(^i+^j)=(1−t)^i+(1−t)^j
We need to find the vectors ¯¯¯¯¯¯¯¯PR and ¯¯¯¯¯¯¯¯¯RQ:
- ¯¯¯¯¯¯¯¯PR=¯¯¯¯¯¯¯¯OR−¯¯¯¯¯¯¯¯OP=((1−t)^i+(1−t)^j)−(45t^i)=(1−t−45t)^i+(1−t)^j=(1−46t)^i+(1−t)^j
For points P,Q,R to be collinear, the vectors ¯¯¯¯¯¯¯¯PR and ¯¯¯¯¯¯¯¯¯RQ must be parallel. This means there exists a scalar λ such that:
¯¯¯¯¯¯¯¯PR=λ¯¯¯¯¯¯¯¯¯RQ
From the vectors we derived:
1. 1−46t=−λ(1−t) (i-component)
2. 1−t=λ(61t−1) (j-component)
From the first equation:
λ=−1−46t1−t
1−t=−1−46t1−t(61t−1)
(1−t)(1−t)=−(1−46t)(61t−1)
(1−2t+t2)=−(61t−1+46t2−46t)
1−2t+t2=−61t+1+46t2
0=45t2−59t
t(45t−59)=0
Since t>0, we have:
t=5945
The value of t that makes points P,Q,R collinear is t=7187.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions
1 Video
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Knowledge Check
The endpoints of ¯¯¯¯¯¯AB are A(0, 0) and B(9, -6). What is an equation of the line that contains the reflection of ¯¯¯¯¯¯AB in the y-axis?
Ay=−32xBy=−23xCy=−x+3Dy=23x

In the figure above, ¯¯¯¯¯¯AB,¯¯¯¯¯¯CD,and¯¯¯¯¯¯EF all intersect. What is the value of n?
View SolutionLet A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP¯¯¯A=14,where ¯¯¯A stands for complement of event A. then , events A and B are
View SolutionLet A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP¯¯¯A=14,where ¯¯¯A stands for complement of event A. then , events A and B are
View Solution
In the diagram above, ¯¯¯¯¯JL=¯¯¯¯¯¯ONand¯¯¯¯¯¯KL=¯¯¯¯¯¯¯OM. Confirmation of which of the following facts would be sufficient to prove that the two triangles are congruent?
View SolutionIf P(A∩B)=12,P(¯¯¯A∩¯¯¯B)=12 and 2P(A)=P(B)=p, then the value of p is equal to
View Solution¯xand¯y be two variable vectors satisfying simultaneous vector equation
¯x+¯cׯy=¯a
¯y+¯cׯx=¯b where ¯c is a non zero vector . Then the value of ¯xand¯y is given by
View Solution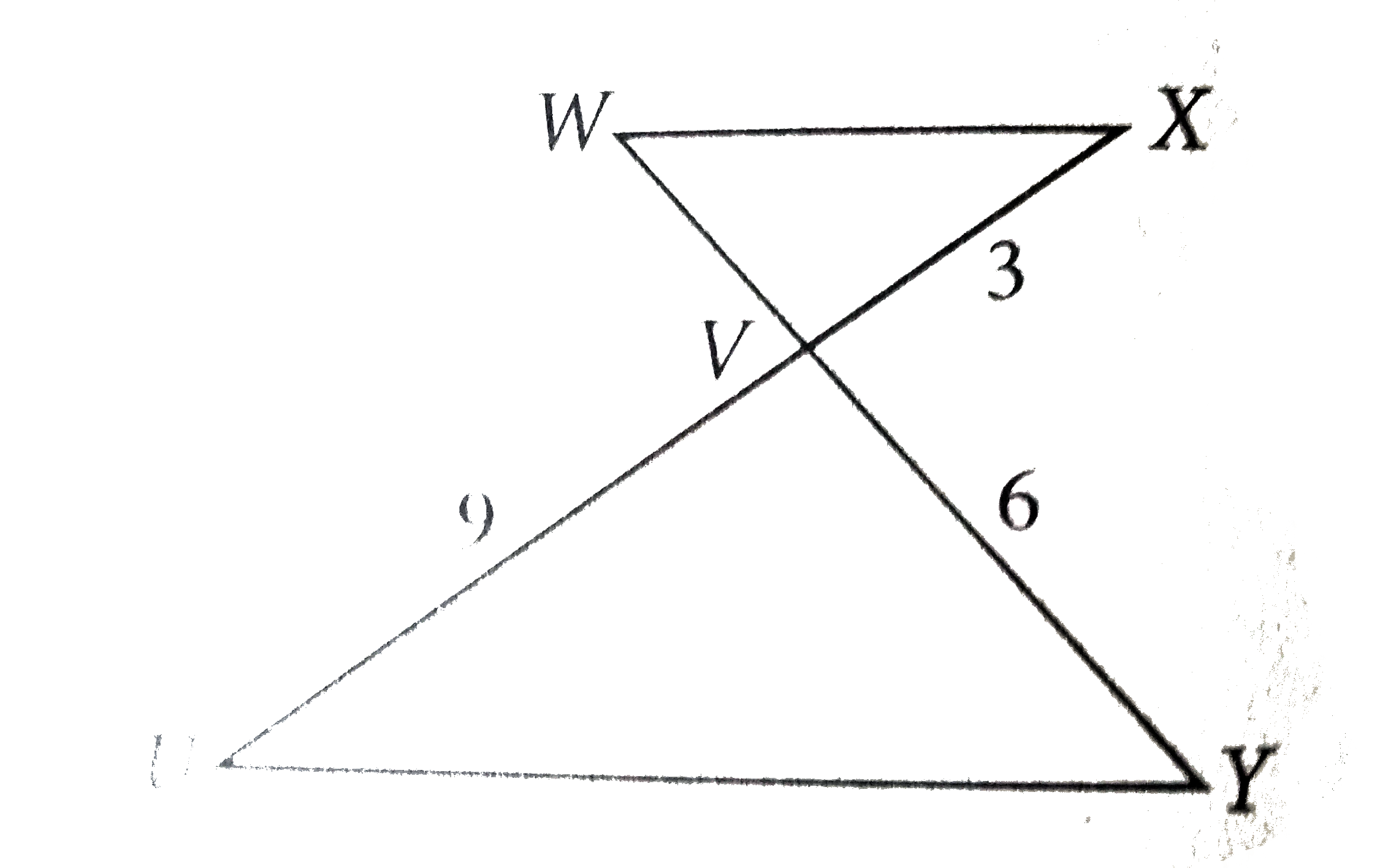
In the figure above, ¯¯¯¯¯¯UYand¯¯¯¯¯¯¯WX are parallel and ¯¯¯¯¯¯UX intersects ovel∈e(WY) at V. What is the length of ¯¯¯¯¯¯¯WY?
View Solution