Katie hikes 5 miles north, 7 miles east, and then 3 miles north again. What number of miles, measured in a straight line, is katie from her starting point?
√83
10
√113
13
The correct Answer is:C
To find the straight-line distance from Katie's starting point to her final position after her hike, we can break down the problem step by step.
Step 1: Determine the total distance traveled in the north direction.
Katie hikes:
- 5 miles north initially
- 3 miles north again
Total distance north = 5 miles + 3 miles = 8 miles
Step 2: Determine the distance traveled in the east direction.
Katie hikes:
- 7 miles east
Total distance east = 7 miles
Step 3: Visualize the problem using a right triangle.
We can visualize Katie's movements on a Cartesian plane:
- The vertical leg of the triangle represents the total distance north (8 miles).
- The horizontal leg of the triangle represents the distance east (7 miles).
Step 4: Apply the Pythagorean theorem.
To find the straight-line distance (hypotenuse) from the starting point to the final position, we can use the Pythagorean theorem:
c=√a2+b2
Where:
- c is the hypotenuse (the distance we want to find),
- a is the vertical leg (8 miles),
- b is the horizontal leg (7 miles).
Substituting the values:
c=√(8)2+(7)2
Step 5: Calculate the squares.
Calculating the squares:
(8)2=64
(7)2=49
Step 6: Add the squares.
Now, add the squares:
64+49=113
Step 7: Take the square root.
Now take the square root to find the hypotenuse:
c=√113
Step 8: Final calculation.
Calculating √113 gives us approximately:
c≈10.63 miles
Conclusion:
Katie is approximately 10.63 miles away from her starting point.
---
Katie hikes:
- 5 miles north initially
- 3 miles north again
Katie hikes:
- 7 miles east
We can visualize Katie's movements on a Cartesian plane:
- The vertical leg of the triangle represents the total distance north (8 miles).
- The horizontal leg of the triangle represents the distance east (7 miles).
To find the straight-line distance (hypotenuse) from the starting point to the final position, we can use the Pythagorean theorem:
- c is the hypotenuse (the distance we want to find),
- a is the vertical leg (8 miles),
- b is the horizontal leg (7 miles).
Calculating the squares:
(7)2=49
Now, add the squares:
Now take the square root to find the hypotenuse:
Calculating √113 gives us approximately:
Katie is approximately 10.63 miles away from her starting point.
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
Beginning in Town A, Biker Bob rode his bike 10 miles west, 3 miles north, 5 miles east, and then 9 miles north to Twon B. How far apart are Twon A and Twon B? (Assume perfectly flat terrain.)
View SolutionA man goes 10 m due east and than 24 m due north. Find the distance from the starting point.
View Solution
Knowledge Check
During a comping trip. Aundria and Annette decide to travel to their campsite using two different routes. Aundria takes the hiking trail that travels 5 miles south, 6 miles east, 7 miles south, and 2 miles west to the campsite, Annette uses the cross-country route that starts at the same point as the kiking trail but goes in a straight line from there to the campsite. About how many miles total will the two travel?
A32.65B33.42C34.00D34.42A car starts a trip with 20 gallons of gas in its tank. The at traveled at an average speed of 65 miles per hour for 3 hours and consumed gas at a rate of 30 miles per gallon. What percent of the gas in the tank was used for the 3-hour trip?
A32.5B33.0C33.5D34.0
Beginning in Town A, Biker Bob rode his bike 10 miles west, 3 miles north, 5 miles east, and then 9 miles north to Twon B. How far apart are Twon A and Twon B? (Assume perfectly flat terrain.)
View SolutionA man goes 10m due east and then 24 m due north. Find the distance from the starting point.
View SolutionA car travles 6km towards north at an angle of 45∘ to the east and then travles distance of 4km towards north at an angle of 135∘ to east (figure). How far is the point from the starting point? What angle does the straight line joining its initial and final position makes with the east?
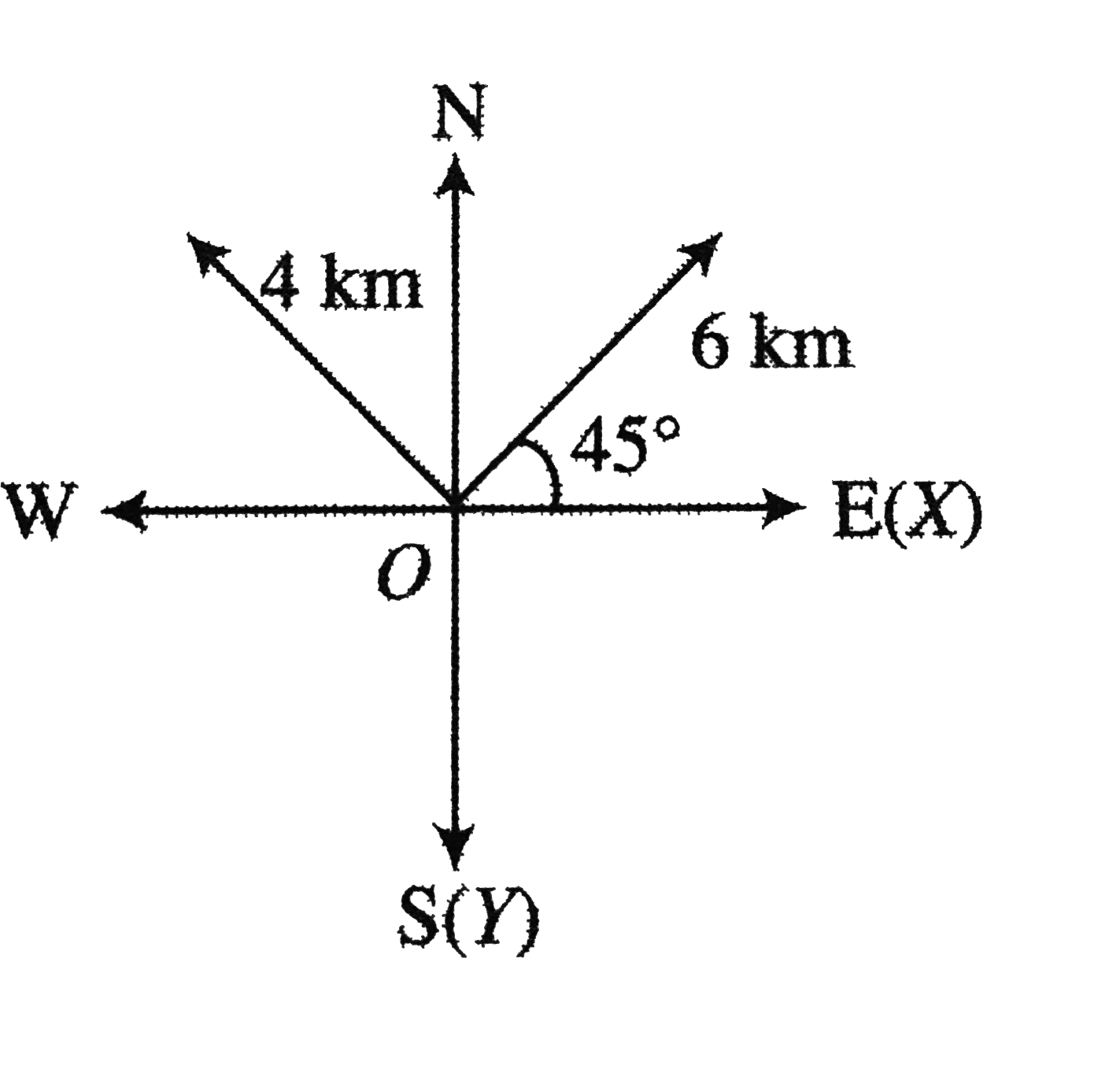
View SolutionA car travles 6km towards north at an angle of 45∘ to the east and then travles distance of 4km towards north at an angle of 135∘ to east (figure). How far is the point from the starting point? What angle does the straight line joining its initial and final position makes with the east?

View SolutionTwo hikers started at the same location. One traveled 2 miles east and then 1 mile north. The other traveled 1 mile west and then 3 miles south. At the end of their hikes, how many miles apart were the two hikers?
View SolutionA man goes 150 m due east and then 200 m due north. How far is he from the starting point ?
View Solution
