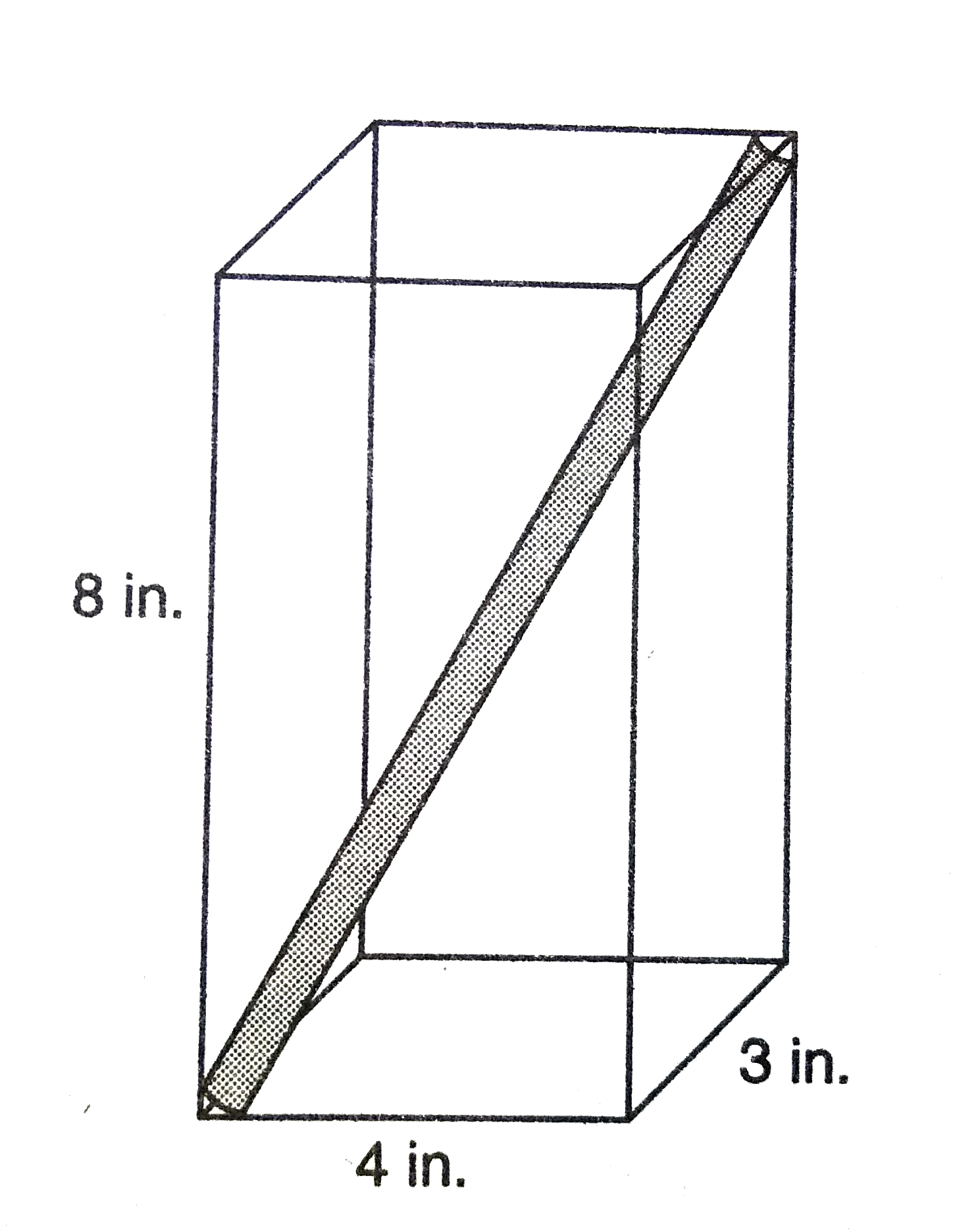
A cylindrical tube with ngligible thichness is placed into a rectangular box that is 3 inches by 4 inches by 8 inches, as shown in the accompanying diagram. If the tubes fits exactly into the box diagonally from the bottom left corner to the top right back corner, what is the best approximately of the number of inches in the length of the cube?
3.9
5.5
7.8
9.4
The correct Answer is:D
Step by step video, text & image solution for A cylindrical tube with ngligible thichness is placed into a rectangular box that is 3 inches by 4 inches by 8 inches, as shown in the accompanying diagram. If the tubes fits exactly into the box diagonally from the bottom left corner to the top right back corner, what is the best approximately of the number of inches in the length of the cube? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions

A box is constructed by cutting 3-inche square from the corner of a square sheet of cardboard, as shown in the accompanying diagram, and then folding the sides up. If the volume of the box is 75 inches, find the number of square inches in the area of the original sheet of cardboard?
View SolutionWhat is the maximum number of boxes with dimensions 2 inches by 3 inches by 4 inches that could fit in a cube-shaped container that has a volume of 1 cubic foot?
View Solution
Knowledge Check
A rectangular box with length 22 inches , width 5 inches , and height 5 inches is to be packed with steel balls of radius 2 inches in such a way that the centers of the balls are collinear. What is the maximum number of balls that can fit into the box, provided that no balls should protrude from the box ?
A0B5C6D10A company ships notepads in rectangular boxes that each have inside dimensions measuring 9 inches long, 9 inches wide, and 12 inches tall. Each notepad is in the shape of a cube with an edge length of 3 inches. What is the maximum number of natepads that will fit in 1 closed box?
A10B11C12D36For Question 19-20 use the figure above

A lamp shade with a circular base is an example of a solid shape called a frustrum. In the figure above, the shaded region represents a frustrum of a right cone in which the portion of the original cone that lies 12 inches below its vertex has been cut off by slicing plane (not shown) parallel to the base.
Q. If the height and slant height of the frustrum are 8 inches and 10 inches, respectively, what is the number of inches in the radius length, R, of the original cone?A9B12C15D8
Jack has a box in the shape of the cube, the inside edges of which are 4 inches long. What is the longest object he could fit inside the box (i.e., What is the diagonal of the cube) ?
View SolutionThe Partside Packing Company needs a rectangular shipping box. The box must have a length of 1 foot, a width of 8 inches, and a volume of at least 700 cubic inches. What is the least number of inches in height of the box such that the height is a whole number?
View SolutionA 3-inch-tall rectangular box with a square base is constructed to hold a circular pie that has a diameter of 8 inches. Both are shown below. What is the volume, in cubic inches, of the smallest such box that can hold this pie?

View SolutionThose who grow up in the Hawaiian Islands learn to swim at a very young age. In fact, the Hawaiian people throw their children in the ocean when they're just starting to walk and let them discover its power. In such circumstances, you learn to swim very quickly out of a sense of self-preservation. One of our favourite swimming holes was a place called Hanauma Bay. The mouth of Hanauma Bay, where it opens into the sea, is approximately three-fourths of a mile wide. Once in the open sea, you can fall prey to what is called the Molokai freight train. It's a very strong and dangerous current, and I don't think there are many swimmers who can swim against it. The water there is probably about 80 to 90 feet deep, and there is no protection from large fish as is usually afforded by oral reefs close to the surface. We would dare one another to swim across the mouth of the bay. When I was eleven or twelve years old I decided to swim it. After all, I had heard all my life, "Hyrum, you can do anything you want to do if you want to do it badly enough." So I went to the left side of the bay. I suddenly found myself diving into the surf and I began to swim across Hanauma Bay. As I look back on it now, it was probably a very foclish thing to do. I had no idea how close I was to the Molokai freight train, but I had great determination. Suddenly I saw a fin gliding through the waves, about 20 yards away and about 8 inches above the water. I swam in a frenzy, a demon in the water. I swam faster, harder, and stronger than I had ever done before or since. I got to the other side of the bay a great deal faster than I had gotten to the middle where I had seen the fin. Shaking from the experience, I looked out over the bay. Running through my mind was my own version of my mother's words: "I knew I could do that. After all, I can do anything I want to do if I want to do it badly enough." Whether or not the fin represented a man-eating shark or a friendly dolphun, or was just a fin of a manta ray gliding by, I will never know. But in my mind I had a great white shark behind me who hadn't eaten for four days and was looking at my white legs in that surf I sat on the rock for some time waiting for the shaking in my legs to stop and thinking about what had just occurred. I had been foolish to try it. But I also felt a surge of euphoria at the accomplishment: I had actually swum across the mouth of Hanauma Bay. That was one of the truly great victories of my life. It has been a source of inspiration on many occasions. Whenever doubts surge into my brain, I still recall that feeling of euphoria while sitting on those rocks overlooking Hanauma Bay. While I have not always lived up to the expectations I have set for myself I feel a degree of inner peace about my ongoing quest to make a difference. Among the things I most strongly feel have made a difference are the principles I have . tried to teach. They will truly help you find out who you really are, what matters most to you, and how to do something about what matters most. Most important, you will find a greater measure of what we all seek in life: inner peace and a sense of fulfilment.
Of course the desired results don't necessarily happen in a day or even a month or a year. They will come imperceptibly, through little daily victories when what matters most truly becomes a part of your everyday life. When those personal victories come, the increase in self-worth, the - sense of well-being, the sense of oneness with oneself are things that no one can take away.
Diving
View SolutionThose who grow up in the Hawaiian Islands learn to swim at a very young age. In fact, the Hawaiian people throw their children in the ocean when they're just starting to walk and let them discover its power. In such circumstances, you learn to swim very quickly out of a sense of self-preservation. One of our favourite swimming holes was a place called Hanauma Bay. The mouth of Hanauma Bay, where it opens into the sea, is approximately three-fourths of a mile wide. Once in the open sea, you can fall prey to what is called the Molokai freight train. It's a very strong and dangerous current, and I don't think there are many swimmers who can swim against it. The water there is probably about 80 to 90 feet deep, and there is no protection from large fish as is usually afforded by oral reefs close to the surface. We would dare one another to swim across the mouth of the bay. When I was eleven or twelve years old I decided to swim it. After all, I had heard all my life, "Hyrum, you can do anything you want to do if you want to do it badly enough." So I went to the left side of the bay. I suddenly found myself diving into the surf and I began to swim across Hanauma Bay. As I look back on it now, it was probably a very foclish thing to do. I had no idea how close I was to the Molokai freight train, but I had great determination. Suddenly I saw a fin gliding through the waves, about 20 yards away and about 8 inches above the water. I swam in a frenzy, a demon in the water. I swam faster, harder, and stronger than I had ever done before or since. I got to the other side of the bay a great deal faster than I had gotten to the middle where I had seen the fin. Shaking from the experience, I looked out over the bay. Running through my mind was my own version of my mother's words: "I knew I could do that. After all, I can do anything I want to do if I want to do it badly enough." Whether or not the fin represented a man-eating shark or a friendly dolphun, or was just a fin of a manta ray gliding by, I will never know. But in my mind I had a great white shark behind me who hadn't eaten for four days and was looking at my white legs in that surf I sat on the rock for some time waiting for the shaking in my legs to stop and thinking about what had just occurred. I had been foolish to try it. But I also felt a surge of euphoria at the accomplishment: I had actually swum across the mouth of Hanauma Bay. That was one of the truly great victories of my life. It has been a source of inspiration on many occasions. Whenever doubts surge into my brain, I still recall that feeling of euphoria while sitting on those rocks overlooking Hanauma Bay. While I have not always lived up to the expectations I have set for myself I feel a degree of inner peace about my ongoing quest to make a difference. Among the things I most strongly feel have made a difference are the principles I have . tried to teach. They will truly help you find out who you really are, what matters most to you, and how to do something about what matters most. Most important, you will find a greater measure of what we all seek in life: inner peace and a sense of fulfilment.
Of course the desired results don't necessarily happen in a day or even a month or a year. They will come imperceptibly, through little daily victories when what matters most truly becomes a part of your everyday life. When those personal victories come, the increase in self-worth, the - sense of well-being, the sense of oneness with oneself are things that no one can take away.
Sense:
View Solution
