Jack has a box in the shape of the cube, the inside edges of which are 4 inches long. What is the longest object he could fit inside the box (i.e., What is the diagonal of the cube) ?
The correct Answer is:4√3 inches
To find the longest object that can fit inside a cube with edge lengths of 4 inches, we need to calculate the space diagonal of the cube. The formula for the diagonal d of a cube with side length a is given by:
d=a√3
Step 1: Identify the side length of the cube.
- The side length a of the cube is given as 4 inches.
Step 2: Substitute the side length into the diagonal formula.
- Using the formula for the diagonal of the cube:
d=a√3
Substituting a=4:
d=4√3
Step 3: Calculate the numerical value of the diagonal.
- To find the approximate value:
√3≈1.732
So,
d≈4×1.732=6.928
Step 4: Round the result to two decimal places.
- The diagonal length can be rounded to:
d≈6.93 inches
Final Answer:
The longest object that could fit inside the box (the diagonal of the cube) is approximately 6.93 inches.
---
- The side length a of the cube is given as 4 inches.
- Using the formula for the diagonal of the cube:
d=a√3
Substituting a=4:
d=4√3
- To find the approximate value:
√3≈1.732
So,
d≈4×1.732=6.928
- The diagonal length can be rounded to:
d≈6.93 inches
The longest object that could fit inside the box (the diagonal of the cube) is approximately 6.93 inches.
Similar Questions
A child has a block in the shape of a cube with one letter written on each face as shown below: (FIGURE) The cube is thrown once. What is the probability of getting (i) A ? (ii) D ?
View SolutionIn figure, a charge q is placed at a distance δ→0 near one of the corners of a cube of edge I on a line of symmetry along diagonal.

1. What is the flux through each of the faces containing the point a?
2. What is the flux through the other three faces?View Solution
Knowledge Check
- Question 1 - Select One
What is the radius of the largest sphere that can be placed inside a cube that has a volume of 64 cubic units?
A2B2√2C4D8 - Question 2 - Select One
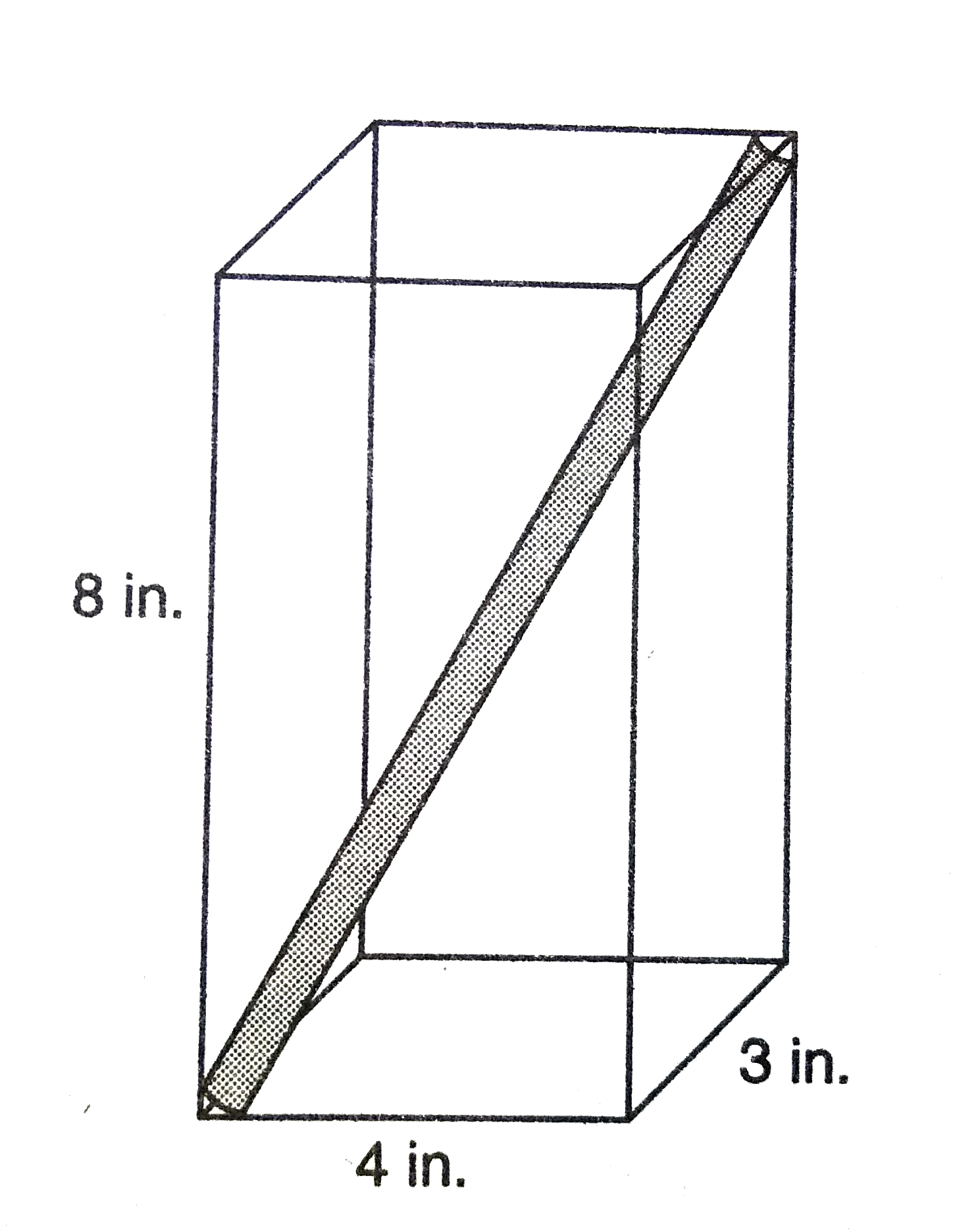
A cylindrical tube with ngligible thichness is placed into a rectangular box that is 3 inches by 4 inches by 8 inches, as shown in the accompanying diagram. If the tubes fits exactly into the box diagonally from the bottom left corner to the top right back corner, what is the best approximately of the number of inches in the length of the cube?A3.9B5.5C7.8D9.4
What is the maximum number of boxes with dimensions 2 inches by 3 inches by 4 inches that could fit in a cube-shaped container that has a volume of 1 cubic foot?
View SolutionRenee has a bag of 6 candies, 4 of which are sweet and 2 of which are sour. Jack picks two candies simultaneously and at random. What is the chance that exactly one of the candies he has picked is sour?
View SolutionMatt has a garden in the shape of a right-angled triangle with one of the acute angles as 30∘ . If the longest side of the triangle is 4 m long, what is the perimeter, in meters , of the garden?
View Solution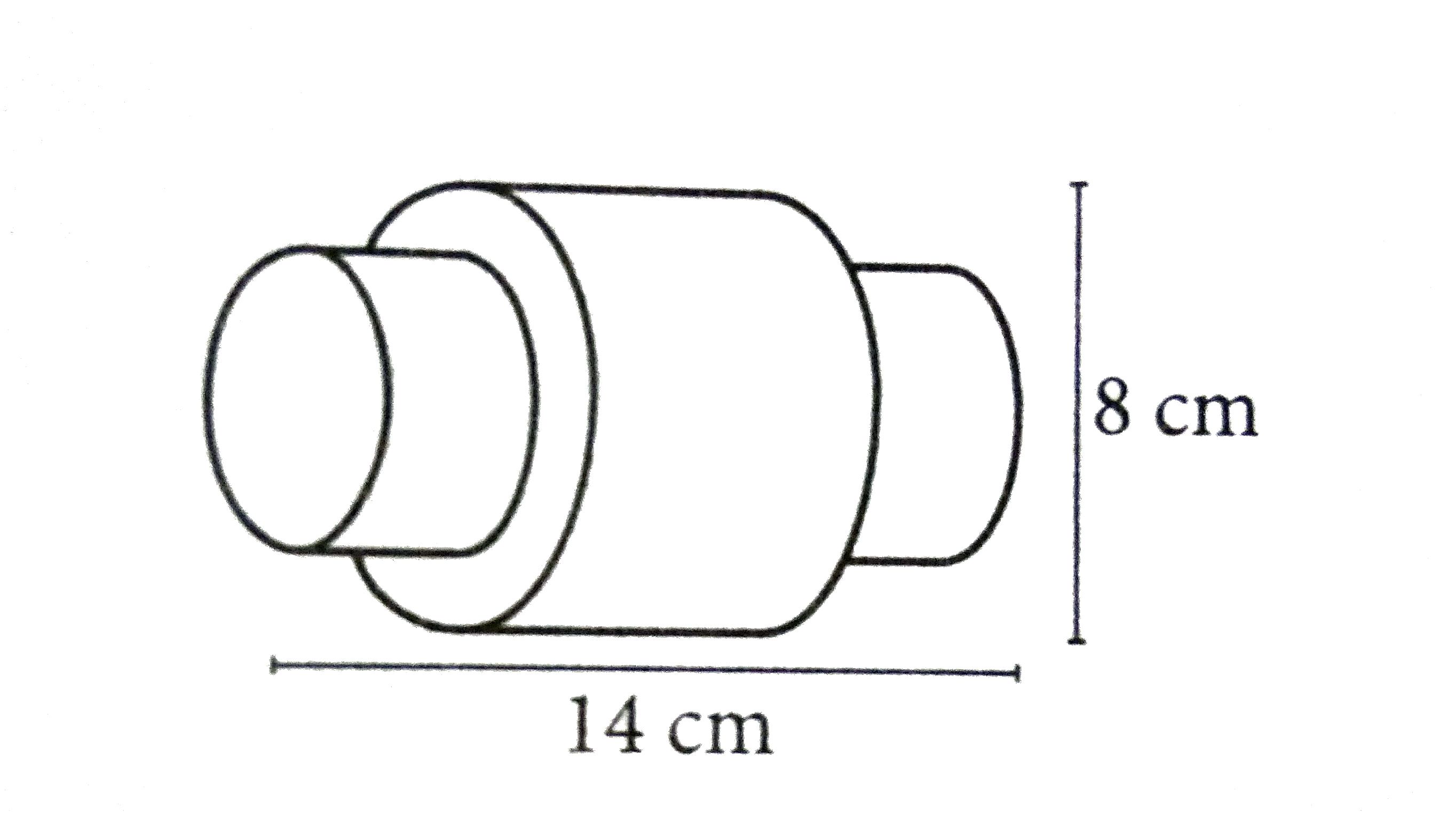
A locking pin is often made using a cylinder-cylinder pair in which a narrow cylinder fits tightly inside a wider cylinder. The inner cylinder protrudes from the outer cylinder, usually by equal amounts on both ends. In the diagram above, the radius of the inner cylinder is half the radius of the outer cylinder by 4 centimeters on each end. What is the volume of the locking pin ? Round your answer to the nearest cubic centimeter.View SolutionAn electric field is uniform, and in the positive x-direction for positive x, and uniform with the same magnitude , but in the negative x-direction for negative x. It is given that
→E=200ˆiN/Cforx>0and→E=−200ˆiN/C for x gt 0. A right circular cylinder of length 20 cm and raidus 5cm has its center at the origin and its axis along the x-axis so that one face is at x=+10cm and the other is at x=−10cm.
(a) What is the net outward flux through the side of the cylinder ? (b) What is the net outward flux through the cyclinder ? (c) what is net charge inside the cylinder ?View SolutionCareful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0×103Nm2/C (a) what is the net charge inside the box ? (b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box ? Why or why not?
View Solution

