
In the figure above, P and Q are the midpoints of sides AB and BC, respectively, of square ABCD. Line segment PB is extended by its own length to point E, and line segment PQ is extended to point F so that FE⊥PE. If the area of square ABCD is 9, what is the area of quadrilateral QBEF?
The correct Answer is:278
Step by step video, text & image solution for In the figure above, P and Q are the midpoints of sides AB and BC, respectively, of square ABCD. Line segment PB is extended by its own length to point E, and line segment PQ is extended to point F so that FEbotPE. If the area of square ABCD is 9, what is the area of quadrilateral QBEF? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Multiple Choice
99 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
In a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

View Solution
Knowledge Check

In rectangle ABCD, point P divide BC such that BP is 25% of the length of BC. If the area of quadrlateral ABPD is 34, what is the area of rectangle ABCD?A156B98C65D32In the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
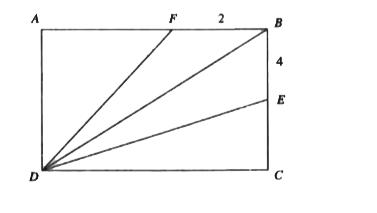 A18B23C30D42
A18B23C30D42
In the diagram below, P and Q are midpoints of sides BC and AD respectively of the parallelogram ABCD. If side AB = diagonal BD: prove that the quadrilateral BPDQ is a rectangle.

View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PB = QC
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
View SolutionP,Q,R and S are the mid points of sides AB,BC , CD and DA respectively of rhombus ABCD. Show that PQRS is a rectangle.
Under what conditions will PQRS be a square ?
View SolutionIn parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
GEHF is a parallelogram.
View SolutionIn parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
triangle HEB and FHC are congruent.
View Solution
