A travel agency sells ship cruises for a popular cruises line. Historically, 135 cruises can be sold when the price is $950 per person. If the price drops to the minimum allowed by the cruises line of $725 per person, 180 cruises can be sold. If the number of cruises sold increase at a constant rate as the price p decrease, where p≥725, which of the following functions best models the situation described?
f(p)=−129p+205
f(p)=−119p+1,135
f(p)=−5p+4,885
f(p)=−15p+325
The correct Answer is:D
To solve the problem, we need to find a linear function that models the relationship between the price of the cruise (p) and the number of cruises sold (N). We have two points based on the information provided:
1. When the price is $950, the number of cruises sold is 135.
2. When the price is $725, the number of cruises sold is 180.
Let's denote the price as p and the number of cruises sold as N. We can represent the two points as:
- Point 1: (950,135)
- Point 2: (725,180)
Step 1: Calculate the slope (m) of the line
The formula for the slope m between two points (x1,y1) and (x2,y2) is given by:
m=y2−y1x2−x1
Here, we will use:
- (x1,y1)=(950,135)
- (x2,y2)=(725,180)
Substituting the values:
m=180−135725−950=45−225=−15
Step 2: Use point-slope form to find the equation
The point-slope form of a linear equation is:
y−y1=m(x−x1)
Using point (950,135) and the slope m=−15:
N−135=−15(p−950)
Step 3: Rearranging to slope-intercept form
Now, we will rearrange the equation to solve for N:
N−135=−15p+9505
Calculating 9505:
9505=190
So the equation becomes:
N−135=−15p+190
Adding 135 to both sides:
N=−15p+190+135
N=−15p+325
Step 4: Final equation
Thus, the function that models the situation is:
N(p)=−15p+325
2. When the price is $725, the number of cruises sold is 180.
- Point 1: (950,135)
- Point 2: (725,180)
The formula for the slope m between two points (x1,y1) and (x2,y2) is given by:
m=y2−y1x2−x1
Here, we will use:
- (x1,y1)=(950,135)
- (x2,y2)=(725,180)
m=180−135725−950=45−225=−15
The point-slope form of a linear equation is:
y−y1=m(x−x1)
Using point (950,135) and the slope m=−15:
N−135=−15(p−950)
Now, we will rearrange the equation to solve for N:
N−135=−15p+9505
Calculating 9505:
9505=190
So the equation becomes:
N−135=−15p+190
Adding 135 to both sides:
N=−15p+190+135
N=−15p+325
Thus, the function that models the situation is:
N(p)=−15p+325
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
When an article is sold without any discount, then its selling price =
Acost priceBmarked priceClist priceDboth (b) and (c) - Question 2 - Select One
A man sold an article for Rs. 396 and gained 10% on it. Find cost price of the article.
ARs 380BRs 340CRs 370DRs 360 - Question 3 - Select One
Carrie's Chocolate shop and Tamika's Treat Shop both sell cadny in boxes. The table below lists the price (the total amount the customer pays) of each box of candy sold at the shops. For each shop, there is a linear relationship between the price of a box of candies and the number of candies in the box. These are the only numbers of candies that can be purchased at the shops.

Which of the following equation gives the relationship between the price in dollars , c, and the number of candies ,n, in a box of cadies at carrie's chocolate shop ?Ac=0.2n+0.5Bc=0.3nCc=0.5n+1.5Dc=n−3.5
If the demand function is p=200−4x, where x is the number of units demanded and p is the price per unit, then MR is
View SolutionThe cost price of 12 oranges is equal to the selling price of 15 oranges. Find the loss per cent.
View SolutionThe selling price of 12 pens is equal to the cost price of 14 pens. Find the gain per cent.
View SolutionA dealer sells a toy for Rs 24 and gains as much per cent as the cost price of the toy. Find the cost price of the toy.
View SolutionThe graph shows the number of music CDs sold at various prices. At what price should the CDs be marked to sell the maximum number of CDs?
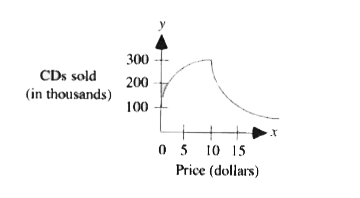 View Solution
View Solution

