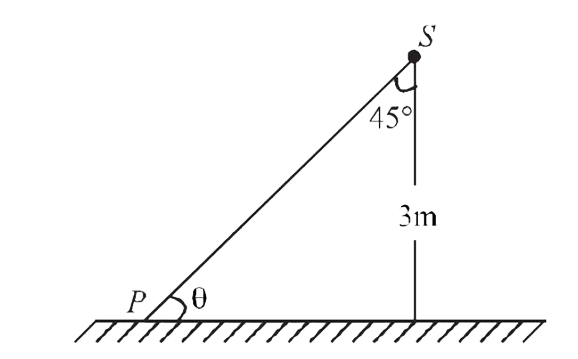
a point source of light is rotating in a horizontal plane at a speed of ω radians/second. There is a wall at a distance d from the source. At some instant the focus of the light is at P and ∠SPN=θ (see figure). Speed of the focus at this instant in terms of θ is 
ωd/cosθ
ωd/sinθ
ωd/tanθ
ωd/sin2θ
The correct Answer is:D
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-225videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-334videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Example127videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
Similar Questions
Spotlight S rotates in a horizontal plane with constant angular velocity of 0.1 radian //second.Thespotoflightpmovesalongthewallatadistanceof3 m .Thevelocityofthespotpwhentheta = 45(@)(see−fig.)is……….. m//s
View SolutionA rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.
View Solution
Knowledge Check
- Question 1 - Select One
A ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M8 at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is 89ω and one fo the masses is at a distance of 35R from O. At this instant the distance of the other mass from O is
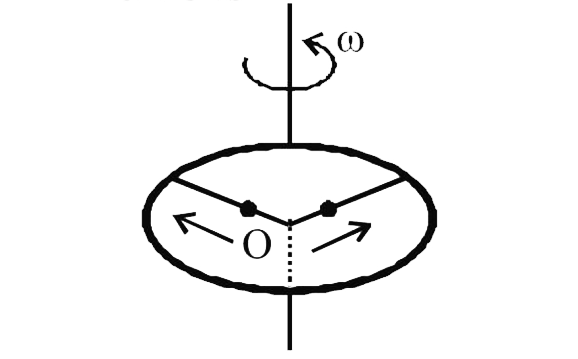A23RB13RC35RD45R - Question 2 - Select One
A point source of light 'S' at a distance d from the screen A produces light intensity I0 at the centre of the screen. If a completely reflecting mirror M is placed at a distance d behind the source as shown in the figure, find the intensity at the centre of the screen
A910I0B109I0C89I0D98I0 - Question 3 - Select One
A beam of light from a source L is incident normally on a plane mirror fixed at a certain distance x from the source. The beam is reflected back as a spot on a scale placed just above the source L. When the mirror is rotated through a small angle θ, the spot of the light is found to move through a distance y on the scale. The angle θ is given by :
AyxBx2yCxyDy2x
A rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.
View SolutionA point source of constant power P is emitting photon of wavelength λ. What is the intensity of photons at r distance from the source ?(speed of light = c)
View SolutionIn the figure shown, O is a point source of light and S is a screen placed at a distance L from the source. Intensity of light at point A on the screen due to the source is 81 I where I is some unit. Now a large mirror (M) is placed behind the source at a distance L from it. The mirror reflects 100% of the light energy incident on it. Calculate the inten- sity at point A.
View SolutionA ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M8 at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is 89ω and one fo the masses is at a distance of 35R from O. At this instant the distance of the other mass from O is
View SolutionA beam of light from a source L is incident normally on a plane mirror fixed at a certain distance x from the source. The beam is reflected back as a spot on a scale placed just above the source L. When the mirror is rotated through a small angle θ the spot of the light is found to move through a distance y on the scale. The angle θ is given by
View Solution