The point of inflection of the curve y=(x−1)3 is Solution in Tamil
(0, 0)
(0, 1)
(1, 0)
(1, 1)
Step by step video & image solution for The point of inflection of the curve y=(x-1)^(3) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATIONS OF DIFFERENTIAL CALCULUSBOOK - SURA PUBLICATIONCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUSEXERCISE - GOVERNMENT EXAM QUESTIONS
7 Videos
- APPLICATIONS OF DIFFERENTIAL CALCULUSBOOK - SURA PUBLICATIONCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUSEXERCISE - ADDITIONAL QUESTIONS
35 Videos
- APPLICATIONS OF DIFFERENTIAL CALCULUSBOOK - SURA PUBLICATIONCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUSEXERCISE - EXERCISE 7.8
11 Videos
- APPLICATION OF MATRICES AND DETERMINANTS BOOK - SURA PUBLICATIONCHAPTER - APPLICATION OF MATRICES AND DETERMINANTS EXERCISE - ADDITIONAL QUESTIONS (5 MARKS)
5 Videos
- APPLICATIONS OF VECTORA ALGEBRABOOK - SURA PUBLICATIONCHAPTER - APPLICATIONS OF VECTORA ALGEBRAEXERCISE - ADDITIONAL QUESTIONS ( 5 MARKS )
5 Videos
Similar Questions
Using Rolle's theorem find the point on the curve y=x2+1,−2≤x≤2 where the tangent is parallel to x-axis.
View SolutionIf a particle moves is a straight line according to s=t3−6t2−15t, the time interval during which the velocity is negative and acceleration is positive is
View SolutionFind two positive numbers whose sum is 12 and their product is maximum.
View SolutionUsing determinants find the quadratic defined by f(x)=ax2+bx+c, if f(1)=0, f(2)=-2 and f(3) = - 6.
View SolutionShow that the points A, B, C with position vector 2ˆi−ˆj+ˆk,ˆi−3ˆj−5ˆkand3ˆi−4ˆj+4ˆk respectively are the vector of a right angled triangle. Also, find the remaining angles of the triangle.
View SolutionNumber of points of inflection of curve y=(x-2)^(6)(x-3)^(5) is
View SolutionIf the point (1,3) serves as the point of inflection of the curve y=ax^(3)+bx^(2) then the value of 'a' and 'b' are -
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
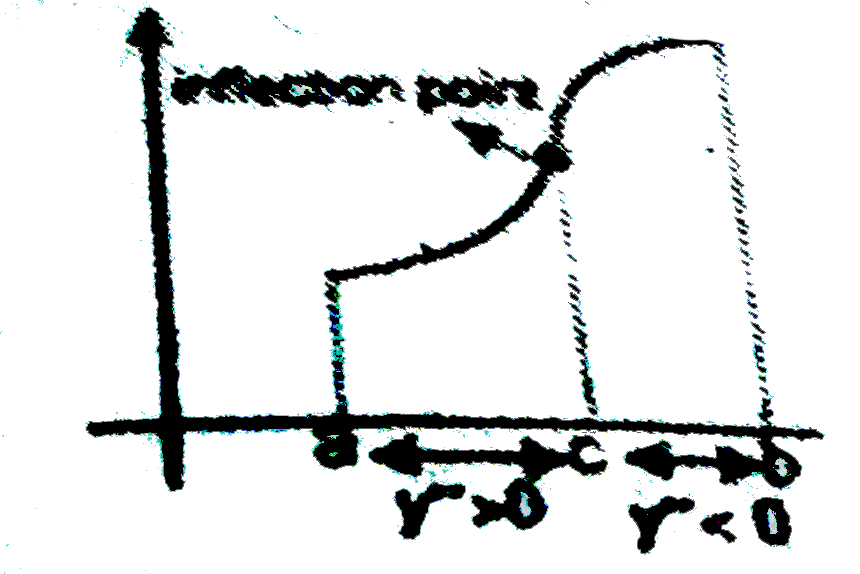
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionConcavity Of Curve And Point Of Inflection
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionFind the inflection points of the curve y=(x−5)5/3+2 .
View SolutionDetermine the intervals of concavity of the curve f(x)=(x−2)3(x−4),x∈R and the points of inflection if any.
View SolutionThe point of inflection of the curve y=x4 is at:
View SolutionFind the points of inflection of y=x4−6x2+8x−1
View SolutionA point of inflection of the curve y=e−x2 is
View Solution
