Find the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
To find the coordinates of the point of inflection of the curve given by the function f(x)=e−x2, we will follow these steps:
Step 1: Find the first derivative f′(x)
Using the chain rule, we differentiate f(x):
f′(x)=ddx(e−x2)=e−x2⋅(−2x)=−2xe−x2
Step 2: Find the second derivative f′′(x)
To find the second derivative, we will use the product rule on f′(x):
f′′(x)=ddx(−2xe−x2)
Using the product rule:
f′′(x)=−2(e−x2+x⋅ddx(e−x2))
We already know ddx(e−x2)=−2xe−x2, so substituting this in gives:
f′′(x)=−2(e−x2−2x2e−x2)=−2e−x2(1−2x2)
Step 3: Set the second derivative equal to zero
For points of inflection, we set f′′(x)=0:
−2e−x2(1−2x2)=0
Since e−x2 is never zero, we simplify to:
1−2x2=0
Solving for x:
2x2=1⟹x2=12⟹x=±1√2
Step 4: Find the corresponding y values
Now we need to find the y values for these x values using the original function:
f(1√2)=e−(1√2)2=e−12=1√e
f(−1√2)=e−(−1√2)2=e−12=1√e
Step 5: Write the coordinates of the points of inflection
The coordinates of the points of inflection are:
(1√2,1√e)and(−1√2,1√e)
Final Answer
The points of inflection are:
(1√2,1√e)and(−1√2,1√e)
---
f′(x)=ddx(e−x2)=e−x2⋅(−2x)=−2xe−x2
f′′(x)=ddx(−2xe−x2)
Using the product rule:
f′′(x)=−2(e−x2+x⋅ddx(e−x2))
We already know ddx(e−x2)=−2xe−x2, so substituting this in gives:
f′′(x)=−2(e−x2−2x2e−x2)=−2e−x2(1−2x2)
−2e−x2(1−2x2)=0
Since e−x2 is never zero, we simplify to:
1−2x2=0
Solving for x:
2x2=1⟹x2=12⟹x=±1√2
f(1√2)=e−(1√2)2=e−12=1√e
f(−1√2)=e−(−1√2)2=e−12=1√e
(1√2,1√e)and(−1√2,1√e)
The points of inflection are:
(1√2,1√e)and(−1√2,1√e)
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Solved Examples
20 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.1
10 Videos
- METHODS OF DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type
46 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
Find the coordinates of the point on the curve, y=x2−1x2+1(x>0) where the gradient of the tangent to the curve is maximum
View SolutionFind the cosine of the angle of intersection of curves f(x)=2x(log)exandg(x)=x2x−1.
View SolutionFind the cosine of the angle of intersection of curves f(x)=2x(log)exandg(x)=x2x−1.
View SolutionThe graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
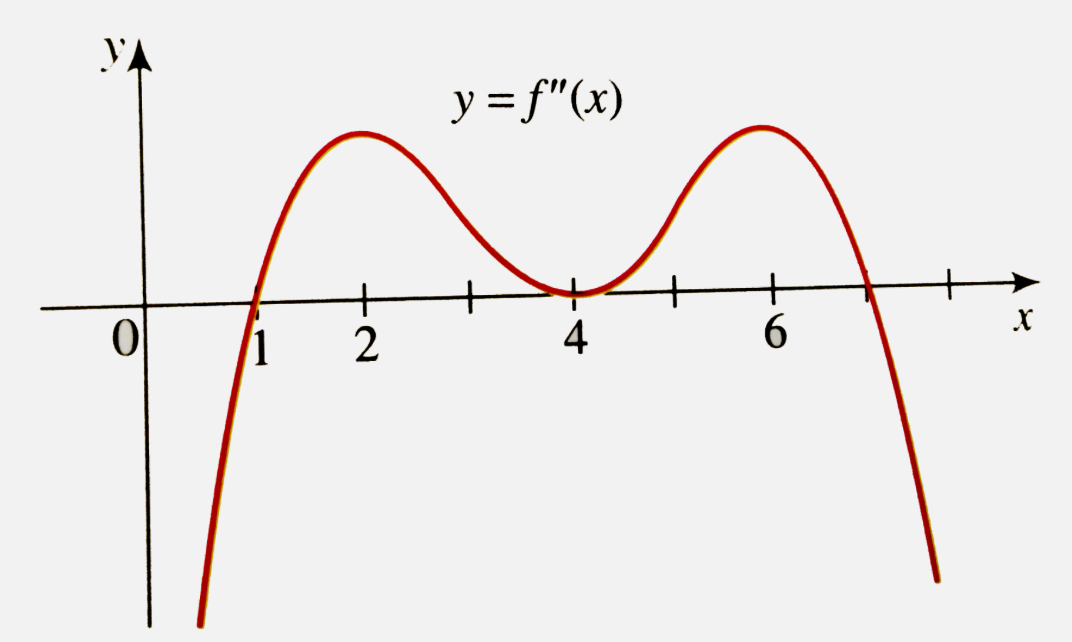
View SolutionFind the coordinates of the point on the curve y=x1+x2 where the tangent to the curve has the greatest slope.
View SolutionFind the coordinates of the points on the curve y=x2+3x+4, the tangents at which pass through the origin.
View SolutionFind the coordinates of the points on the curve y=x2+3x+4 , the tangents at which pass through the origin.
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1 . Also, find the corresponding local maximum and local minimum values
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1. Also, find the corresponding local maximum and local minimum values.
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1 . Also, find the corresponding local maximum and local minimum values
View Solution
