Assuming all the surfaces to be smooth, find the acceleration of the triangular block of mass M when the block of mass m slides on it.

When the block of mass m slides in downward direction, the triangular block will move towards left.

Let the acceleration of triangular block w.r.t. the ground be a0
Acceleration of the block w.r.t. to the triangular block =a (as shown)
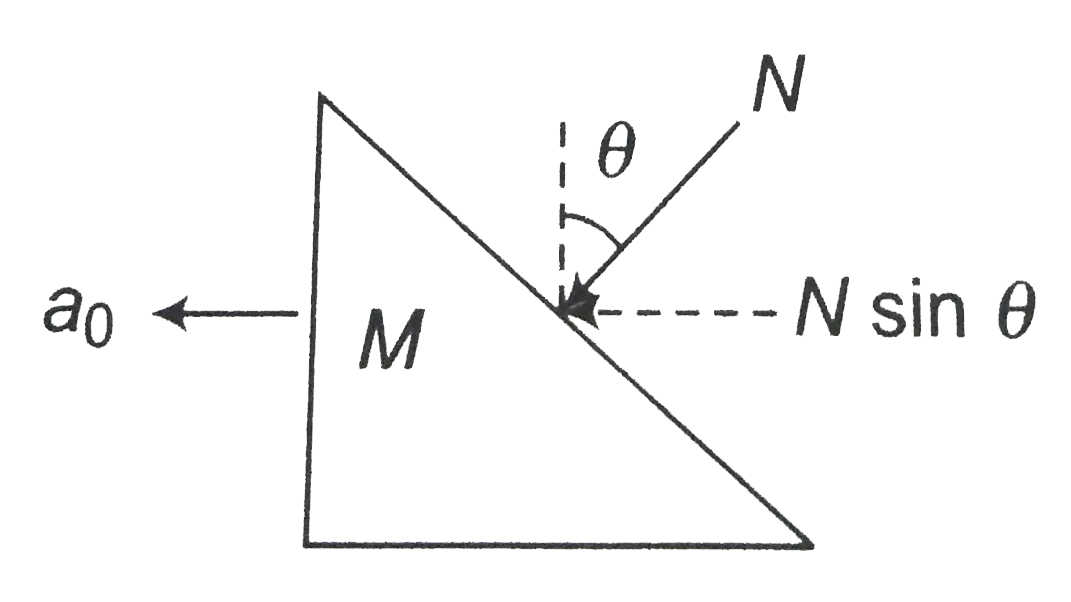
←Nsinθ=Ma0 (i)
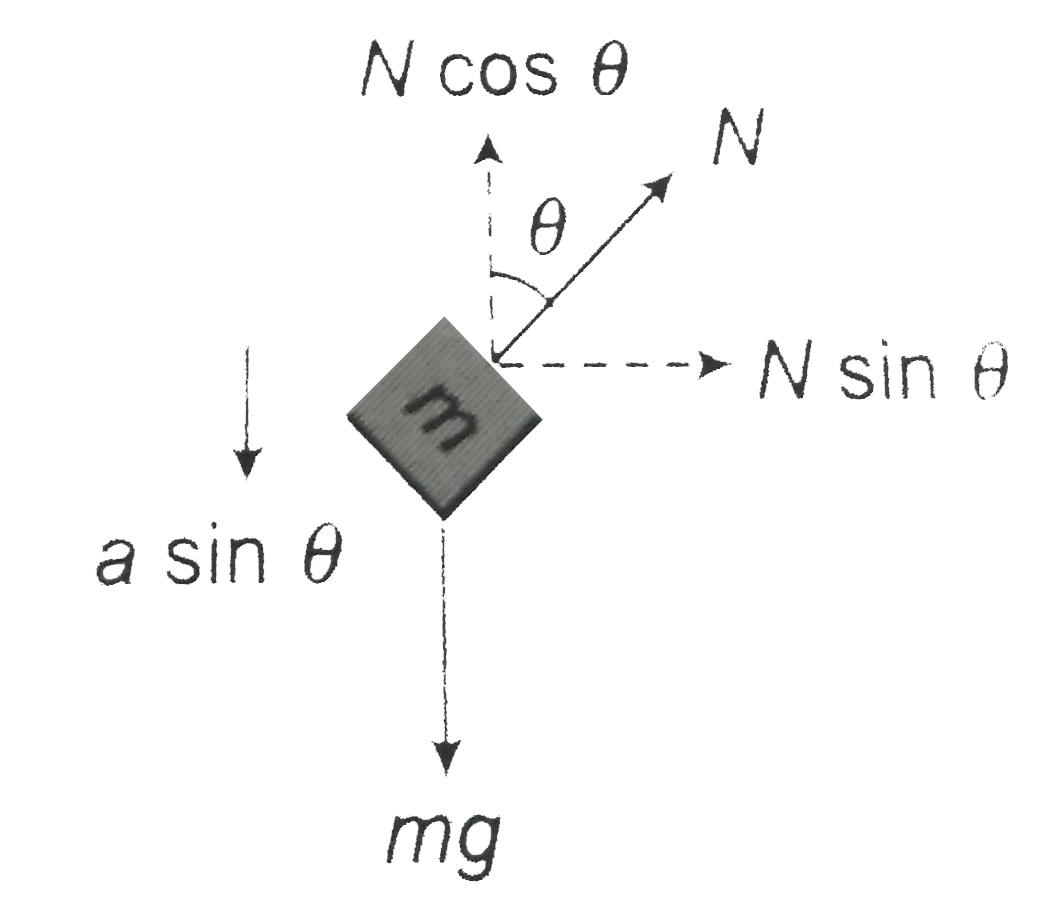
→Nsinθ=m(acosθ−a0) (ii)
↓:mg−Ncosθ=masinθ (iii)
Solving a0=mgsinθcosθM+msin2θ
OR
If we consider the motion of m along the plane, for this break a0 into component along and ⊥ar to the plane.
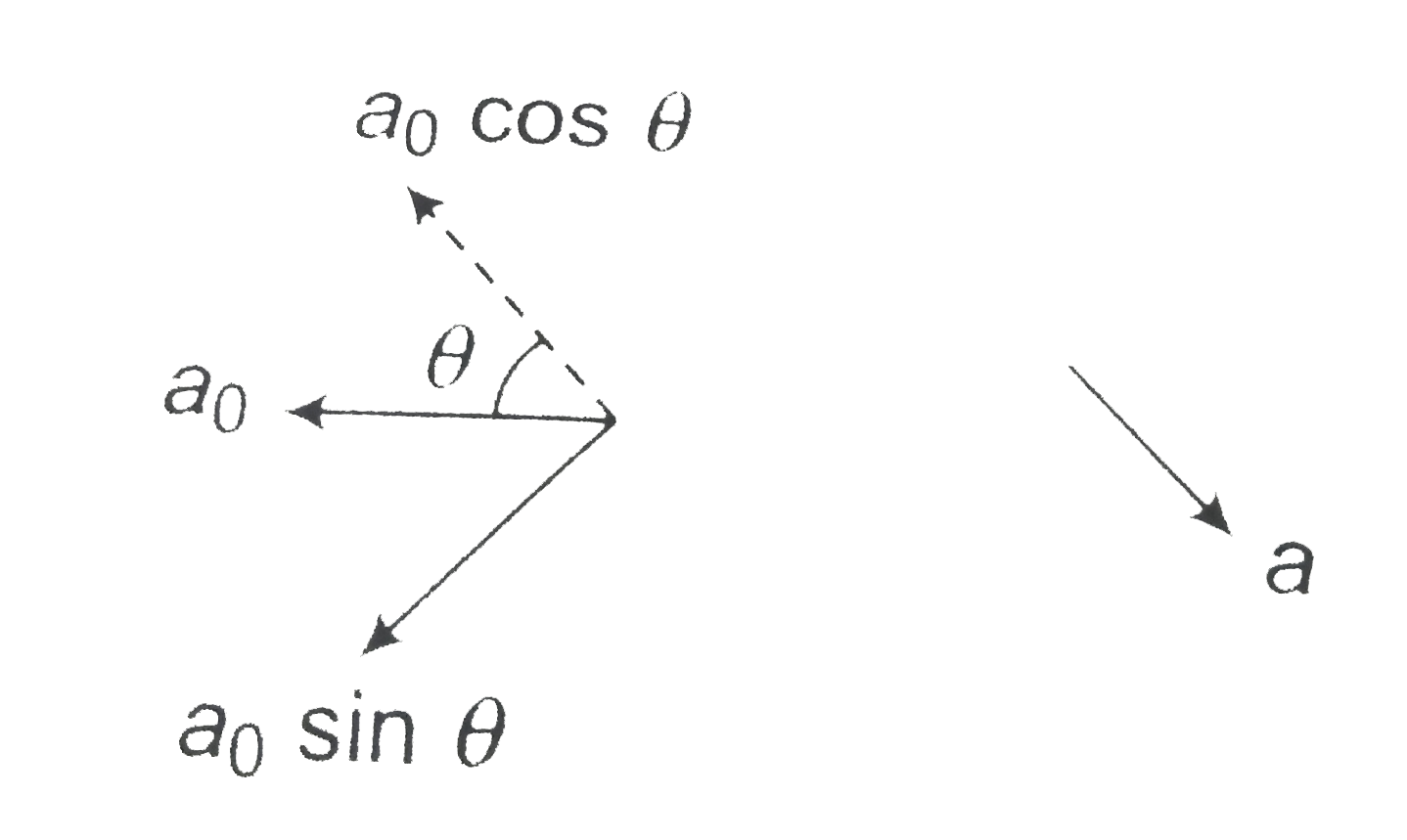
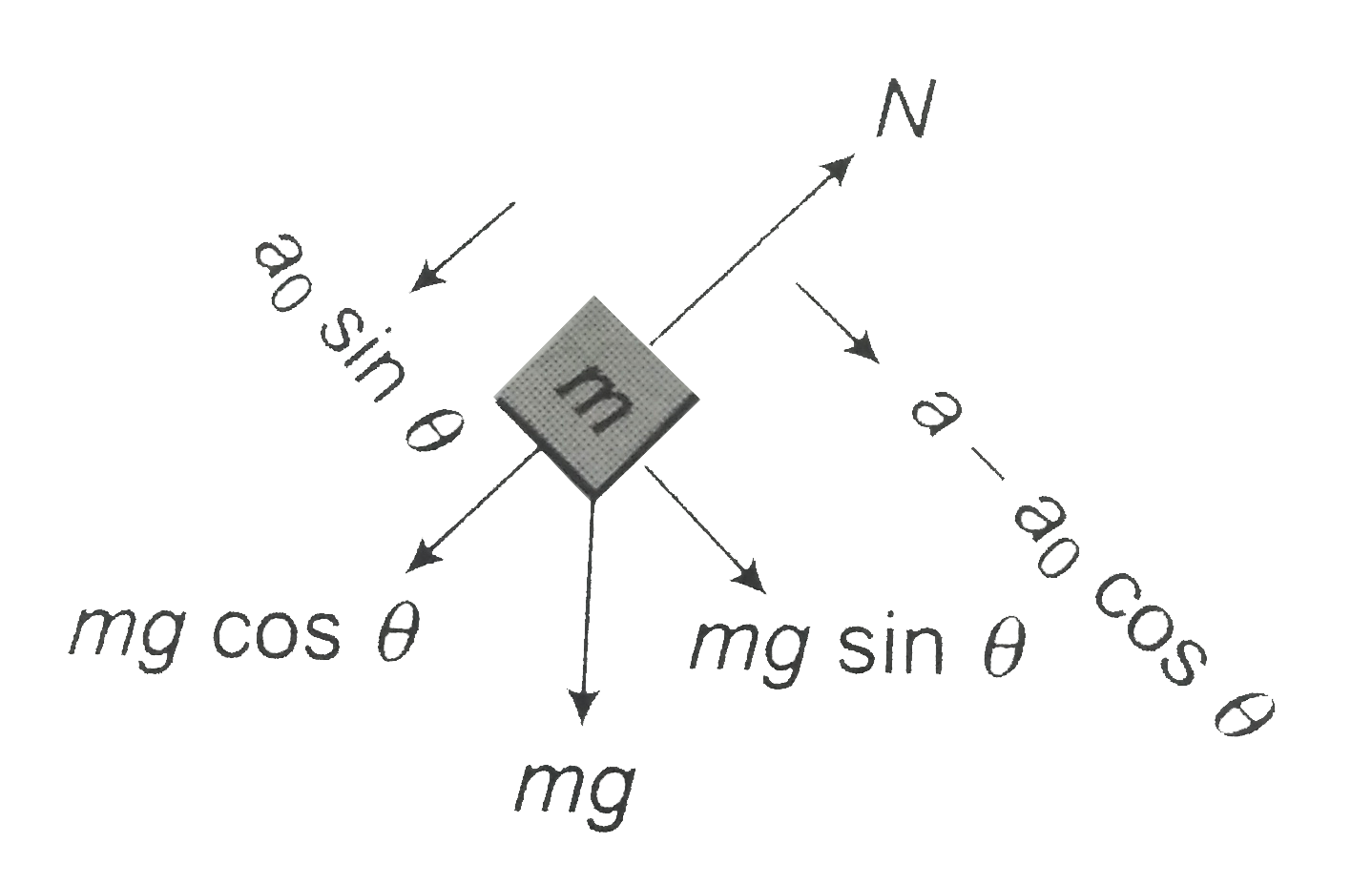
Along the plane: mgsinθ=m(a−a0cosθ) (i)
⊥ar to the plane: mgcosθ−N=ma0sinθ (ii)
Solving (i) and (ii), we get
a0=mgsinθcosθM+msin2θ
OR
For smaller block, if we work from the reference frame attached to the triangular block (a non−inertial frame, because the triangular block is acceleration with acceleration a0) we have to apply a psuedo force ma0 on the small block towards right.
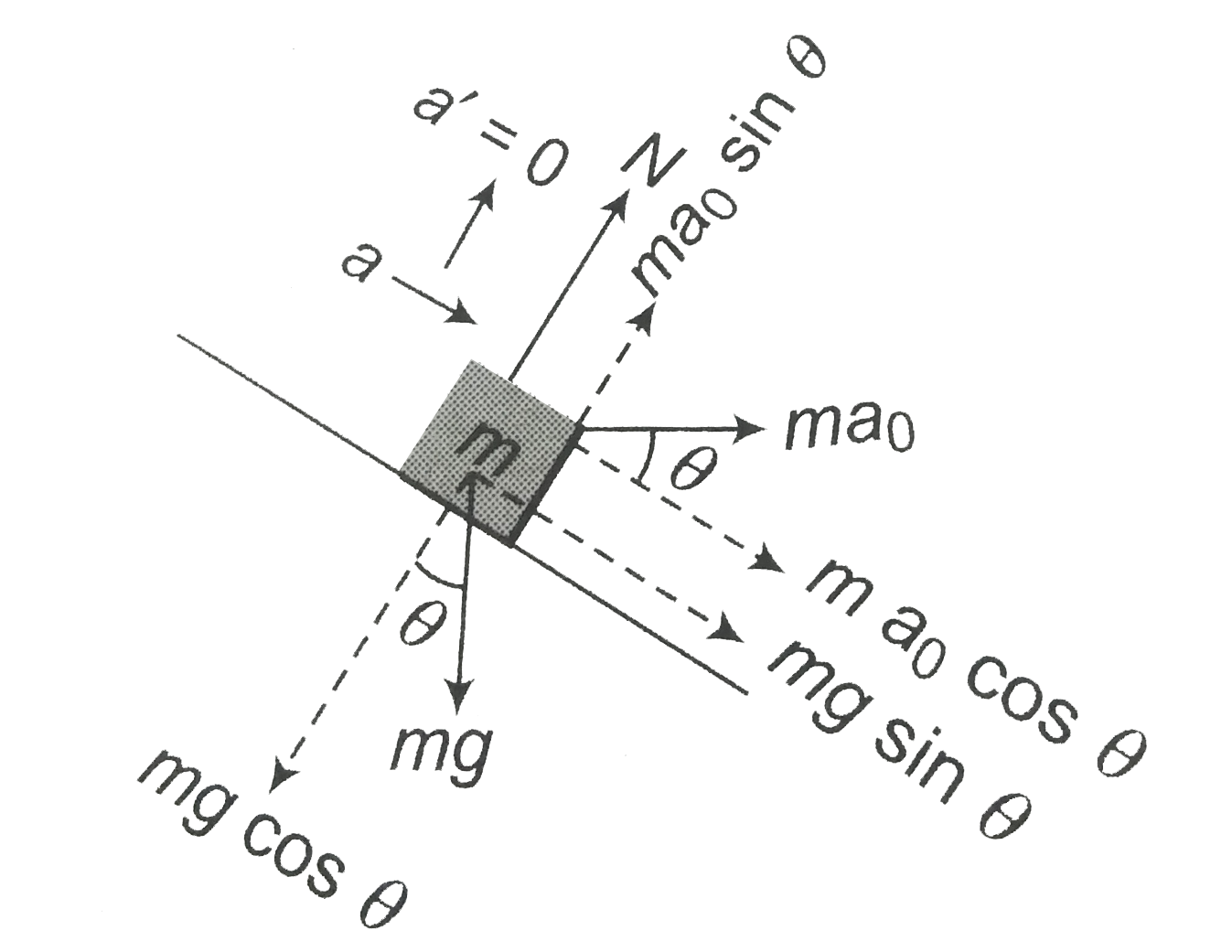
⊥ar to the plane: N+ma0sinθ−mgcosθ=ma'=0
N=mgcosθ−ma0sinθ
For M:Nsinθ=ma0
(mgcosθ−ma0sinθ)sinθ−Ma0
mgsinθcosθ=M(M+msin2θ)a0
a0=mgsinθcosθM+msin2θ
Topper's Solved these Questions
Similar Questions
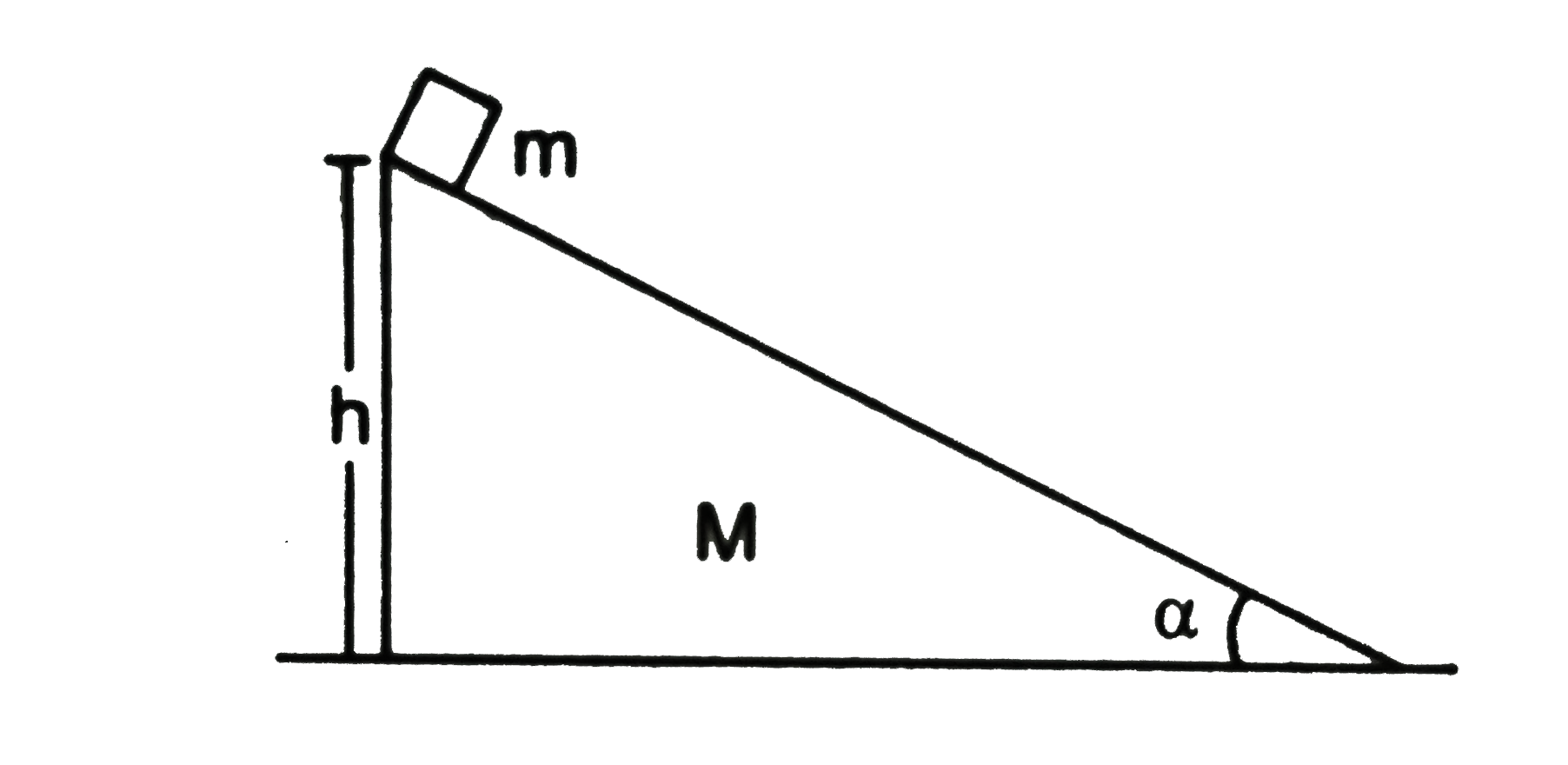
A block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
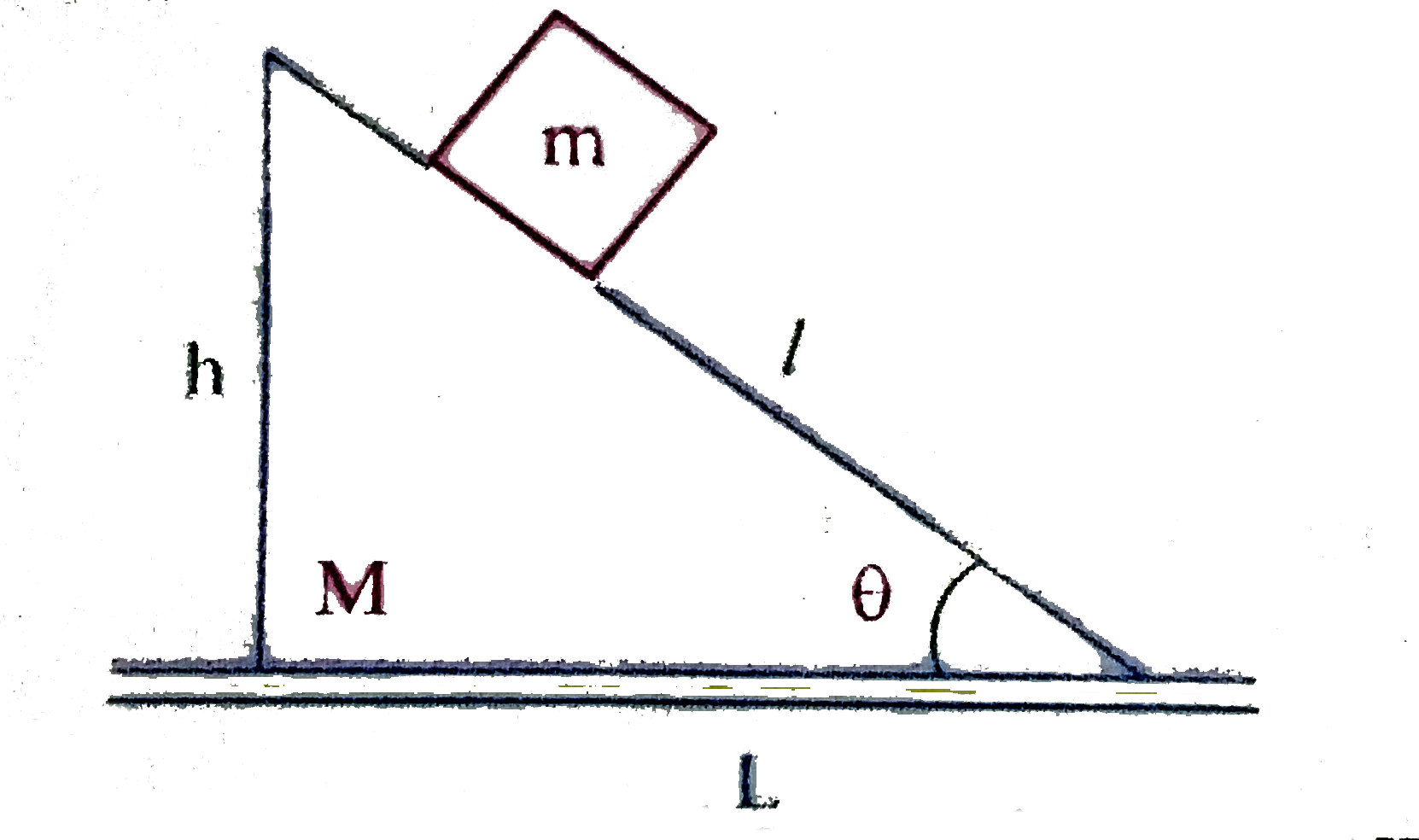
View SolutionAll surfaces are smooth Find the horizontal displacements of the block and the wedge when the block slides down from top to bottom
 .
.
View Solution
Knowledge Check
Find the acceleration of the block of mass m. Assume pulleys are massless and frictionless.
 Ag/3B2g3Cg2DNone
Ag/3B2g3Cg2DNoneTwo blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
A(m2−m1m1+m2)gB(m1+m2m1−m2)gC(m1+m2m1−m2)gD(m1−m2m1+m2)2g
A block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

View SolutionFind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless.

View SolutionIn the given arrangement all surfaces are smooth. What acceleration should be given to the system, for which the block m2 doesn't slide down?

View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.

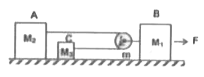
View SolutionThree blocks, placed on smooth horizontal surface are connected by ideal string and a disc shaped pulley of radius r, and mass m. Find the accelerations of the blocks. Masses of the blocks are given as M1=10kg,M2=5kg,M3=2kg,m=2kg.
View Solution
