ABC is a part of ring having radius R2 and ADC is a part of disc having inner radius R1 and outer R2. Part ABC and ADC have same mass. Then center of mass will be located, from the centre.

(R2−R1)(2R1+R2)3π(R1+R2)(above)
(R2−R1)(2R1+R2)3π(R1+R2)(below)
2R1+R23π(above)
2R1+R23π(below)
The correct Answer is:A
Step by step video, text & image solution for ABC is a part of ring having radius R_(2) and ADC is a part of disc having inner radius R_(1) and outer R_(2). Part ABC and ADC have same mass. Then center of mass will be located, from the centre. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-221videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-3,(P-1)5videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Example50videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
Similar Questions
A metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
 View Solution
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View Solution
Knowledge Check
- Question 1 - Select One or More
A solid spher of mass m1 density ρ1 radius R1 and a solid cone of mass m2 density ρ2. Radius R2, are arranged as shown in the figure. The centre of mass is located at
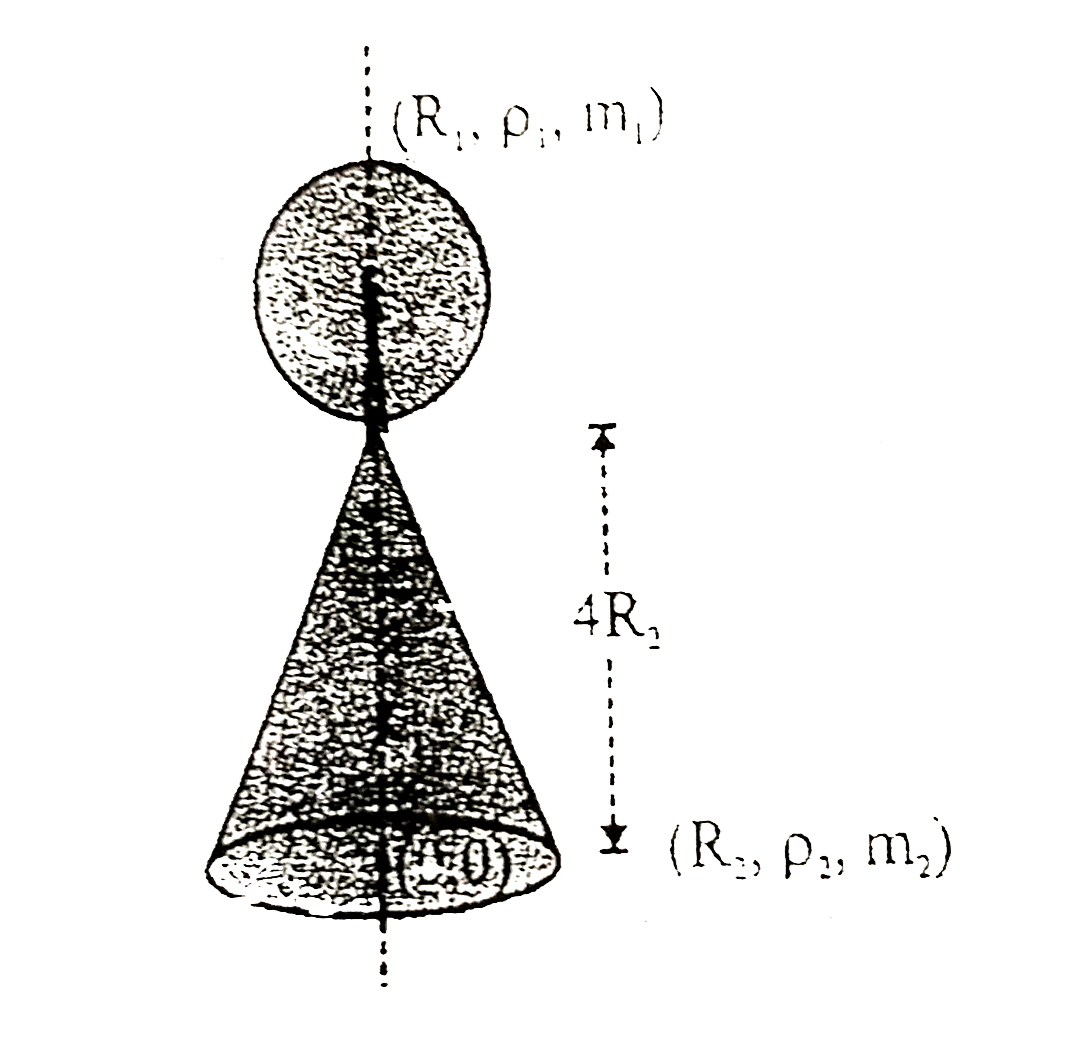 A(0, 3R) if m1=m2=m and R1=R2=RB(0, 3R) if ρ1=ρ2 and R1=R2=RC(0,11R3) if ρ1=2ρ2 and R1=R2=RDalways at (0,4R2)
A(0, 3R) if m1=m2=m and R1=R2=RB(0, 3R) if ρ1=ρ2 and R1=R2=RC(0,11R3) if ρ1=2ρ2 and R1=R2=RDalways at (0,4R2) - Question 2 - Select One
A point charge Q is located at the centre of a hollow spherical conductor having inner radius as R1 and outer radius R2. The conductor being uncharged initially. The potential at the inner surface will be
AKQ[1R1+1R2]BKQ[1R1−1R2]CKQ[1R2−1R1]Dnone of these - Question 3 - Select One
In the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
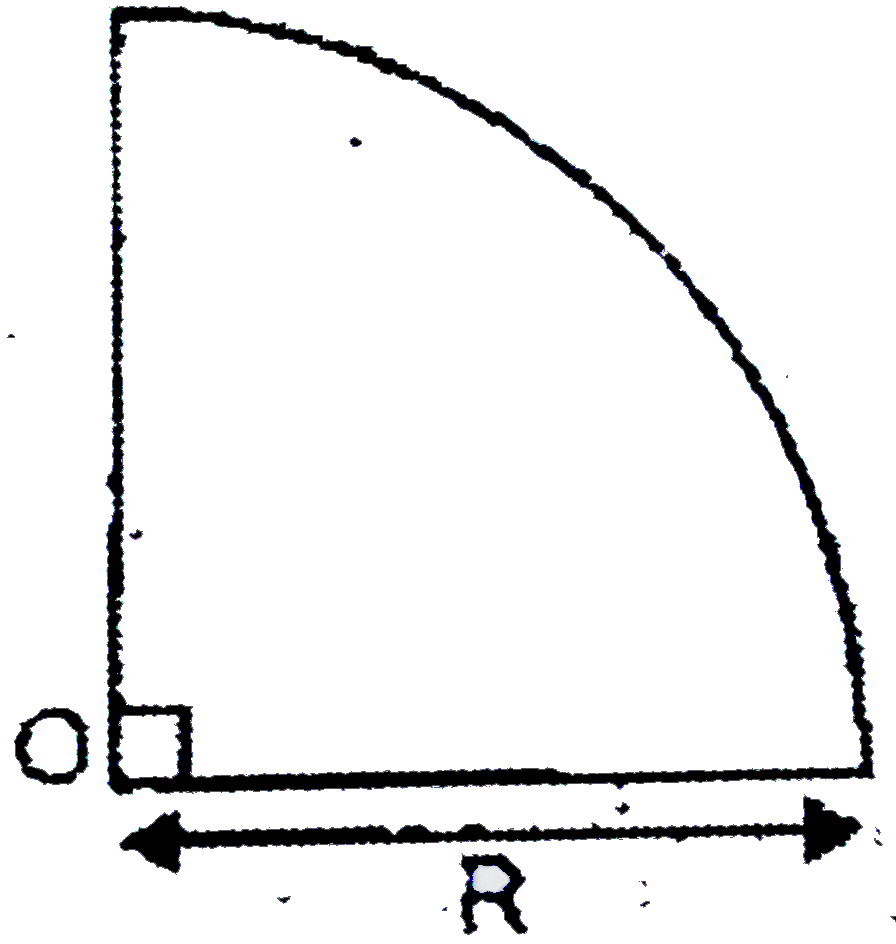 A4R3πB2r3πC√24R3πD√22R3π
A4R3πB2r3πC√24R3πD√22R3π
A metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charges 'Q' A charges 'q' is placed at the centre of the shell.
What is the surface charges density on the (i) inner surface (ii) outer surface of the shell?
(b) A spherical conducting shell of inner radius r1 and outer radius r2 has a charges 'Q' A charges 'q' is placed at the centre of the shell.
Write the expression for the electric field at a point x>r2 from the centre of the shell.View SolutionThe moment of inertia of a flat angular ring having mass M, inner radius a and outer radius b about the diametric axis through the centre is
View SolutionThe moment of inertia of a flat angular ring is having mass M, inner radius a and outer radius b about the perpendicular axis through the centre is
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the center of the shell. Find the electric potential at the center of the shell.
View Solution

