A billiard table whose length and width are as shown in the figure. A ball is placed at point A. at what angle θ the ball be projected so that after colliding with two walls, the ball will fall in the pocket B? assume that all collisions are perfectly elastic: (neglect friction)

The correct Answer is:A
Topper's Solved these Questions
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-2
21 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-3,(P-1)
5 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Example
50 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type
13 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN
12 Videos
Similar Questions
Velocity of the ball A after collision with the ball B as shown in the figure is (Assume perfectly inelastic and head - on collision)
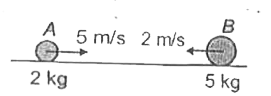
View SolutionFive balls are placed one after the other along a straight line as shown in the figure. Initially, all the balls are at rest. Then the second ball has been projected with speed v0 towards the third ball. Mark the correct statements, (Assume all collisions to be head-on and elastic.)
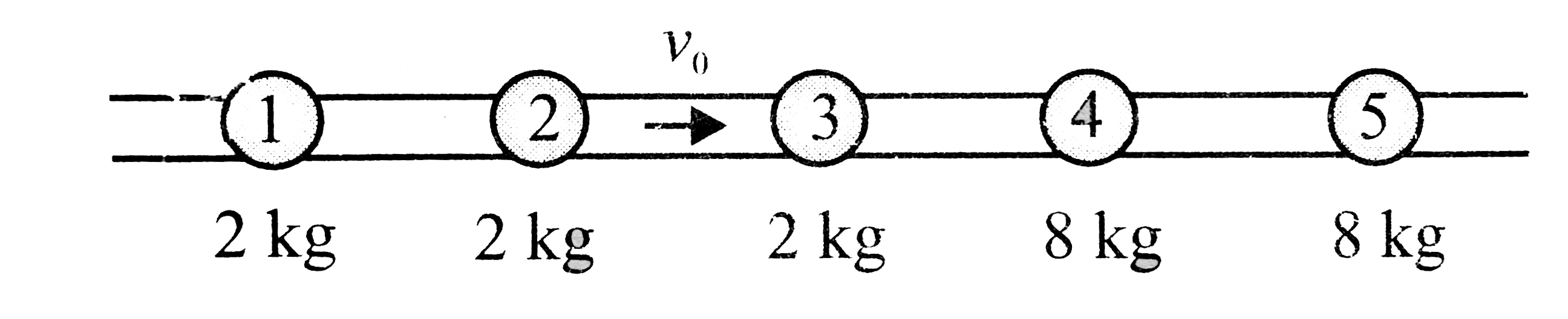
View Solution
Knowledge Check
Velocity of the ball A after collision with the ball B as shown in the figure is (Assume perfectly inelastic and head - on collision)
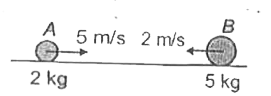 A37m/sB57m/sC17m/sDZero
A37m/sB57m/sC17m/sDZeroFive balls are placed one after the other along a straight line as shown in the figure. Initially, all the balls are at rest. Then the second ball has been projected with speed v0 towards the third ball. Mark the correct statements, (Assume all collisions to be head-on and elastic.)
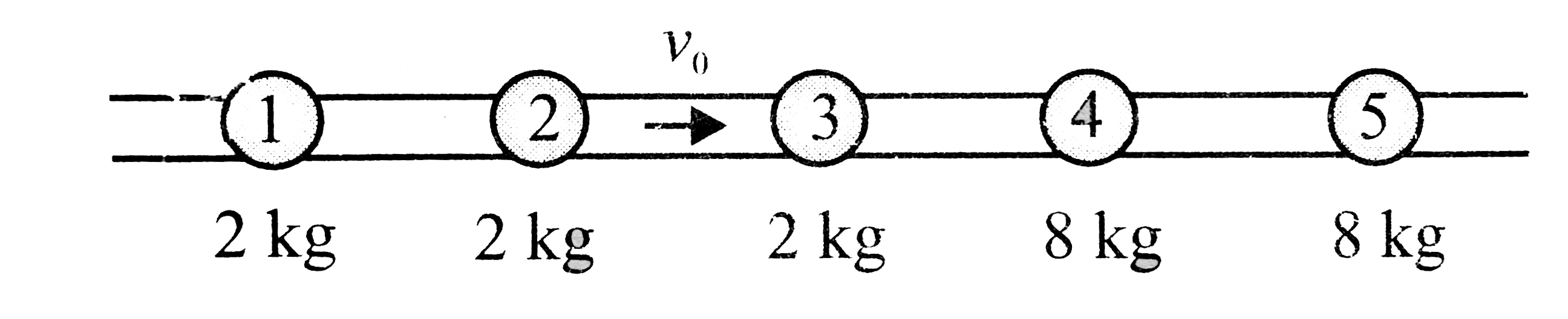 ATotal number of collisions in the process is 5BVelocity of separation between the first and fifth ball after the last possible collision is v0CFinally, three balls remain stationary.DAll of the above
ATotal number of collisions in the process is 5BVelocity of separation between the first and fifth ball after the last possible collision is v0CFinally, three balls remain stationary.DAll of the above
Consider the collision depicted in Figure, to be between two billiard balls with equal masses m1=m2. The first ball is called the cue and the second ball is called the target. The billiard player wants to sink the target ball in a corner pocket, which is at an angle θ2=ϕ=37∘. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain θ1=θ .
View SolutionThe figure below shows three identical balls A , B and C. Initially , the baiis B and C are at rest and the ball A while moving with a veiocity v, collides with ball B. if the collision is perfectiy elastic , then after the collision

View SolutionThe figure below shows three identical balls A , B and C. Initially , the baiis B and C are at rest and the ball A while moving with a veiocity v, collides with ball B. if the collision is perfectiy elastic , then after the collision

View SolutionA solid spherical ball rolling without slipping collides elastically with an identical ball at rest, as shown in the figure. Assuming that the frictional forces are small enough to have negligible effect during the instant of collision, calculate, the velocity of each ball along enough time after the collision when each ball is again rolling without slipping.
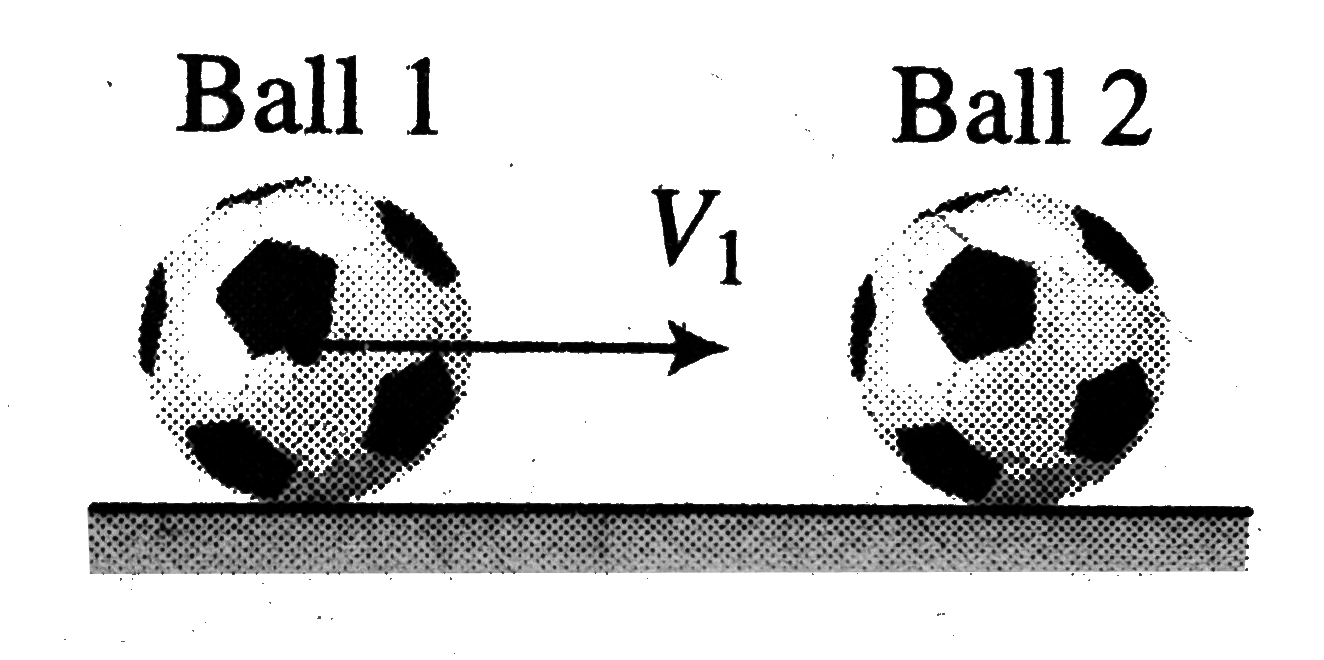
View SolutionA solid spherical ball rolling without slipping collides elastically with an identical ball at rest, as shown in the figure. Assuming that the frictional forces are small enough to have negligible effect during the instant of collision, calculate, the velocity of each ball along enough time after the collision when each ball is again rolling without slipping.

View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View Solution
