Consider the collision depicted in Figure, to be between two billiard balls with equal masses m1=m2. The first ball is called the cue and the second ball is called the target. The billiard player wants to sink the target ball in a corner pocket, which is at an angle θ2=ϕ=37∘. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain θ1=θ .
To solve the problem of finding the angle θ1=θ for the collision between two billiard balls, we will use the principles of conservation of momentum and conservation of kinetic energy, as the collision is elastic. Here are the steps to derive the solution:
1. Identify the Variables:
- Let the mass of both balls be m1=m2=m.
- The initial velocity of the cue ball (ball 1) is u1=U and it is moving at an angle θ with respect to the x-axis.
- The target ball (ball 2) is initially at rest, so its initial velocity u2=0.
- After the collision, let the velocity of ball 1 be v1 at an angle θ and the velocity of ball 2 be v2 at an angle ϕ=37∘.
2. Conservation of Momentum:
- The momentum before the collision must equal the momentum after the collision. In vector form, this can be expressed as:
m⋅U=m⋅v1+m⋅v2
- Since the masses are equal, we can simplify this to:
U=v1+v2
3. Conservation of Kinetic Energy:
- For an elastic collision, the total kinetic energy before the collision must equal the total kinetic energy after the collision:
12mU2=12mv21+12mv22
- Simplifying this gives:
U2=v21+v22
4. Using the Dot Product:
- From the conservation of momentum, we can express the squares of the velocities in terms of their dot products:
U2=v21+v22+2v1v2cos(θ+ϕ)
- Substituting U2 from the kinetic energy equation gives:
v21+v22=v21+v22+2v1v2cos(θ+ϕ)
- This simplifies to:
0=2v1v2cos(θ+ϕ)
- Since v1 and v2 cannot be zero, we have:
cos(θ+ϕ)=0
5. Finding the Angles:
- The cosine is zero when θ+ϕ=90∘. Given that ϕ=37∘:
θ+37∘=90∘
- Solving for θ gives:
θ=90∘−37∘=53∘
Final Answer:
θ1=θ=53∘
- Let the mass of both balls be m1=m2=m.
- The initial velocity of the cue ball (ball 1) is u1=U and it is moving at an angle θ with respect to the x-axis.
- The target ball (ball 2) is initially at rest, so its initial velocity u2=0.
- After the collision, let the velocity of ball 1 be v1 at an angle θ and the velocity of ball 2 be v2 at an angle ϕ=37∘.
- The momentum before the collision must equal the momentum after the collision. In vector form, this can be expressed as:
m⋅U=m⋅v1+m⋅v2
- Since the masses are equal, we can simplify this to:
U=v1+v2
- For an elastic collision, the total kinetic energy before the collision must equal the total kinetic energy after the collision:
12mU2=12mv21+12mv22
- Simplifying this gives:
U2=v21+v22
- From the conservation of momentum, we can express the squares of the velocities in terms of their dot products:
U2=v21+v22+2v1v2cos(θ+ϕ)
- Substituting U2 from the kinetic energy equation gives:
v21+v22=v21+v22+2v1v2cos(θ+ϕ)
- This simplifies to:
0=2v1v2cos(θ+ϕ)
- Since v1 and v2 cannot be zero, we have:
cos(θ+ϕ)=0
- The cosine is zero when θ+ϕ=90∘. Given that ϕ=37∘:
θ+37∘=90∘
- Solving for θ gives:
θ=90∘−37∘=53∘
θ1=θ=53∘
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems
27 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.
54 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A billiard table whose length and width are as shown in the figure. A ball is placed at point A. at what angle θ the ball be projected so that after colliding with two walls, the ball will fall in the pocket B? assume that all collisions are perfectly elastic: (neglect friction)

View SolutionA tennis ball with (small) mass m2 rests on the top of a basketball of mass m1which is at a height h above the ground, and the bottom of the tennis ball is at height h+d above the ground. The balls are dropped. To what height does the tennis ball bounce with respect to ground? (Assume all collisions to be elastic and m1>>m2)
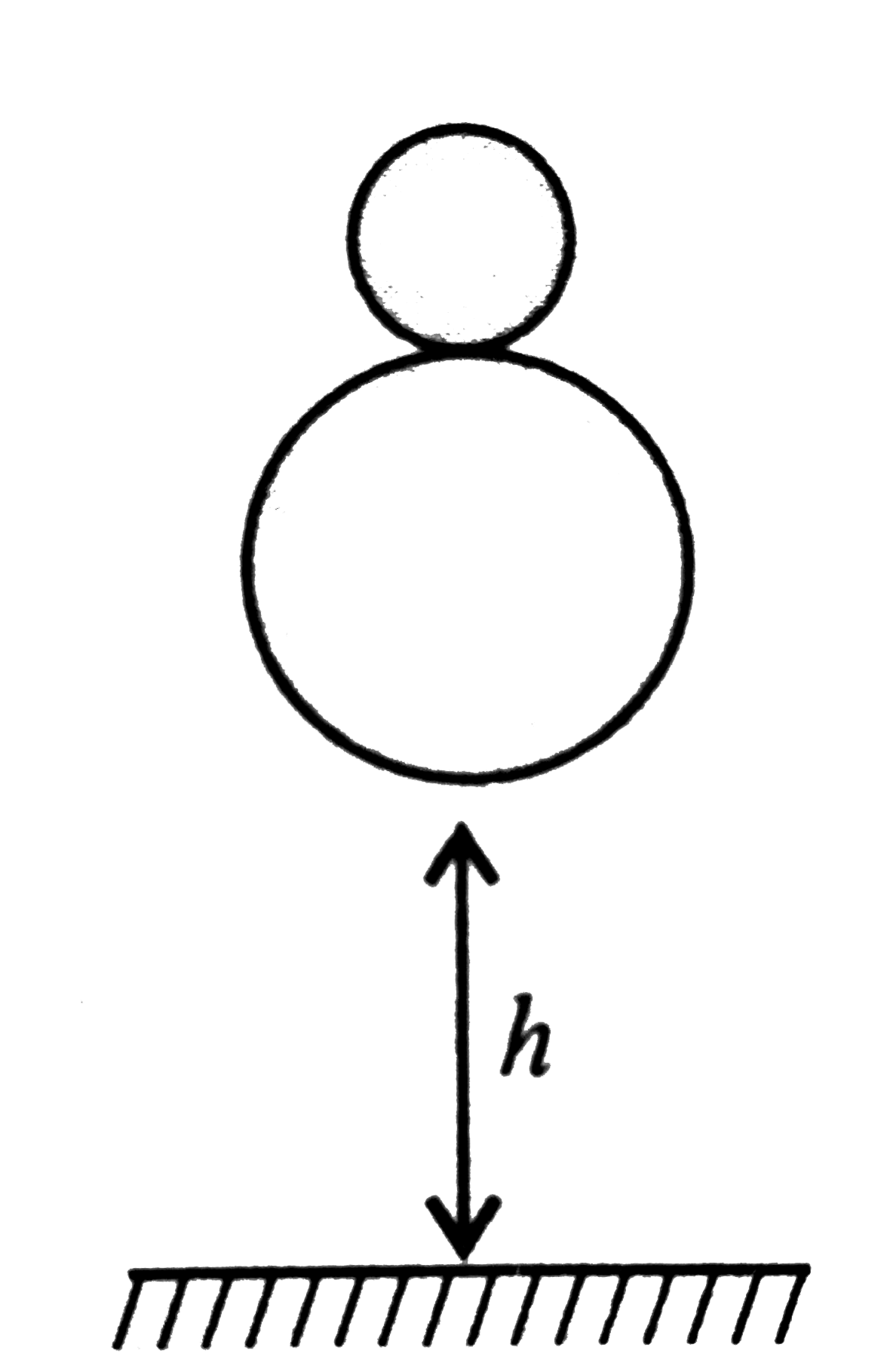
View Solution
Knowledge Check
A billiards player hits a stationary ball by an identical ball to pocket the target ball in a corner pocket that is at an angle of 35∘ with respect to the direction of motion of the first ball. Assuming the collision as elastic and that friction and rotational motion are not important, the angle made by the target ball with repect to the incoming ball is
A35∘B50∘C55∘D60∘Which one of the following statement does not hold good when two balls of masses m1 and m2 undergo elastic collision
AWhen m1<<m2 and m2 at rest, there will be maximum transfer of momentumBWhen m1>>m2andm2 at rest, after collision the ball of mass m2 moves with four times the velocity of m1CWhen m1=m2 and m2 at rest, there will be maximum transfer of K.E.DWhen collision is oblique and m2 at rest with m1=m2 after collision the balls move in opposite direction.A spherical ball of mass m1 colliddes head on with another ball of mass m2 at rest . The collision is elastic . The fraction of kintic energy lost by m1 is :
A4m1m2(m1+m2)2Bm1m1+m2Cm2m1+m2Dm1m2(m1+m2)2
A particle of mass m is projected towards a wall such that theangle of incidence is θ and the speed just before collision is u. Assumming that the wall is smooth and the collision is elastic,show that the ball rebonunds at same angle.
View Solution
A small ball of mass m2 rests on the top of a bigger ball of mass m1(>>m2. The centre of bigger ball is at height 3r above ground as shown. The balls are dropped from this situation. If the smaller ball bounces to a height 4 nr from ground after its first collision with bigger ball. find n. (Assume all collisions are elastic).
View SolutionTwo balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
View SolutionWhich one of the following statement does not hold good when two balls of masses m1andm2 undergo elastic collision
View SolutionTwo billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured?
View Solution