P is a point at a distance r from the centre of a solid sphere of radius a. The gravitational potential at P is V. IF V is plotted as a function of r, which is the correct curve ?
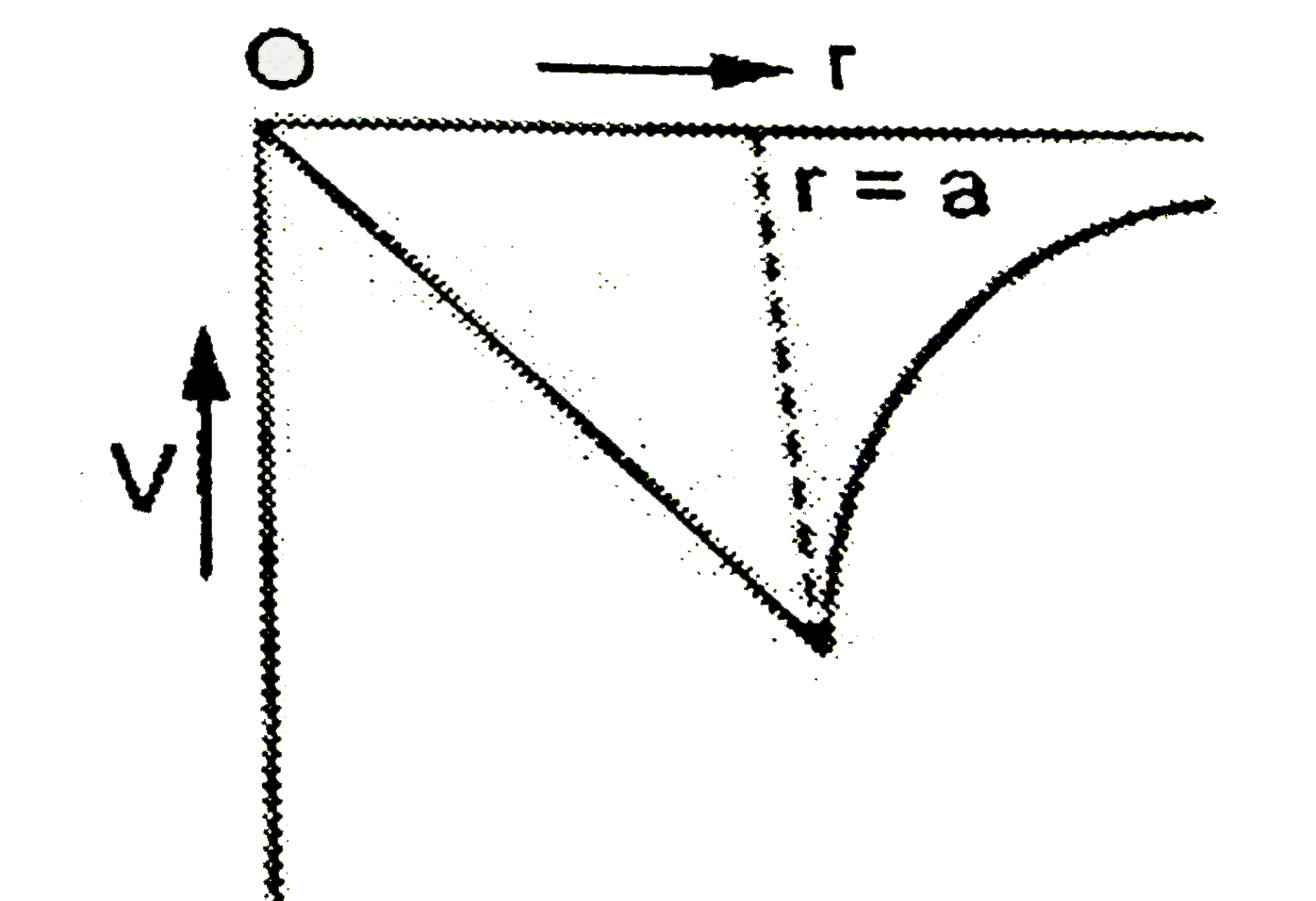
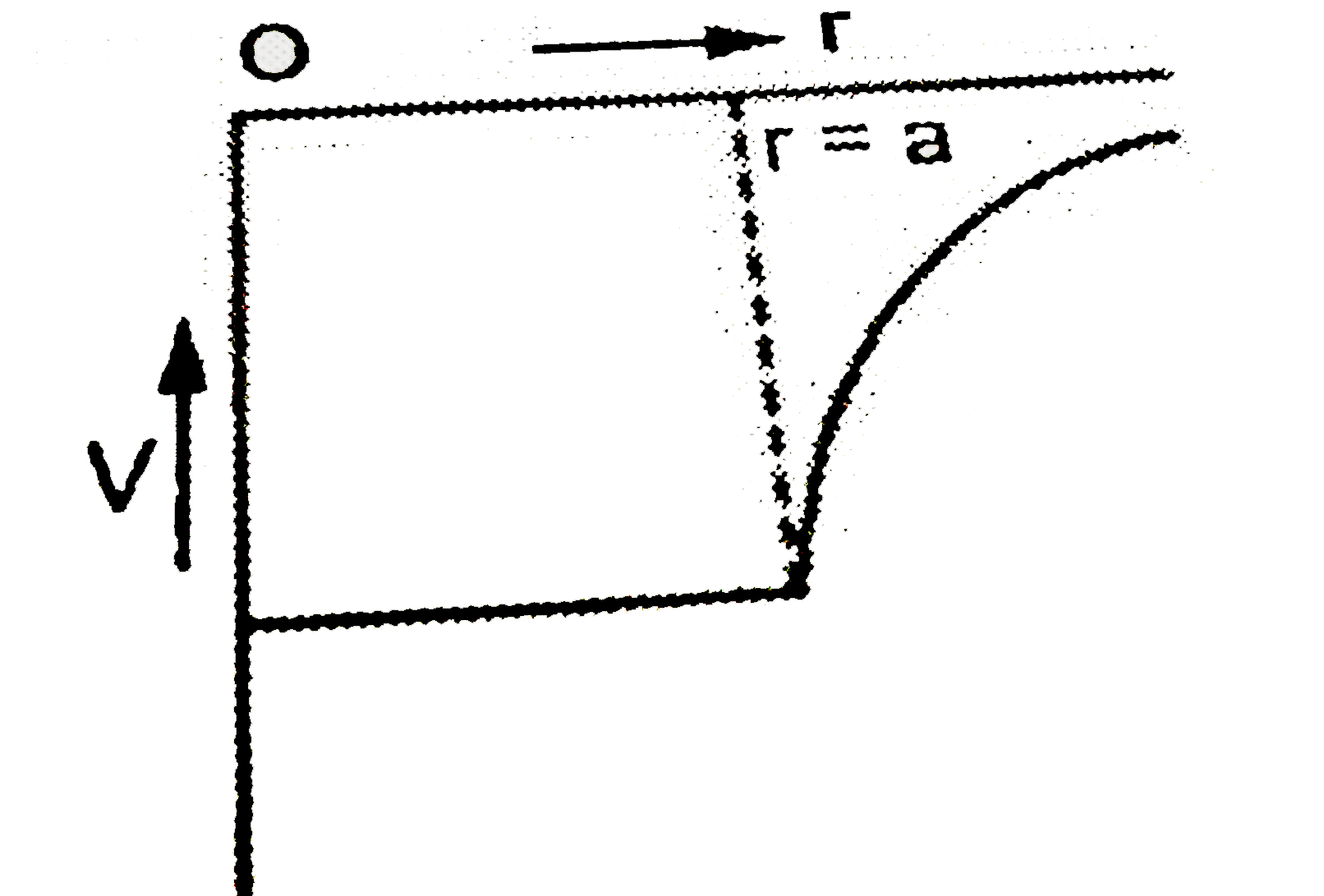
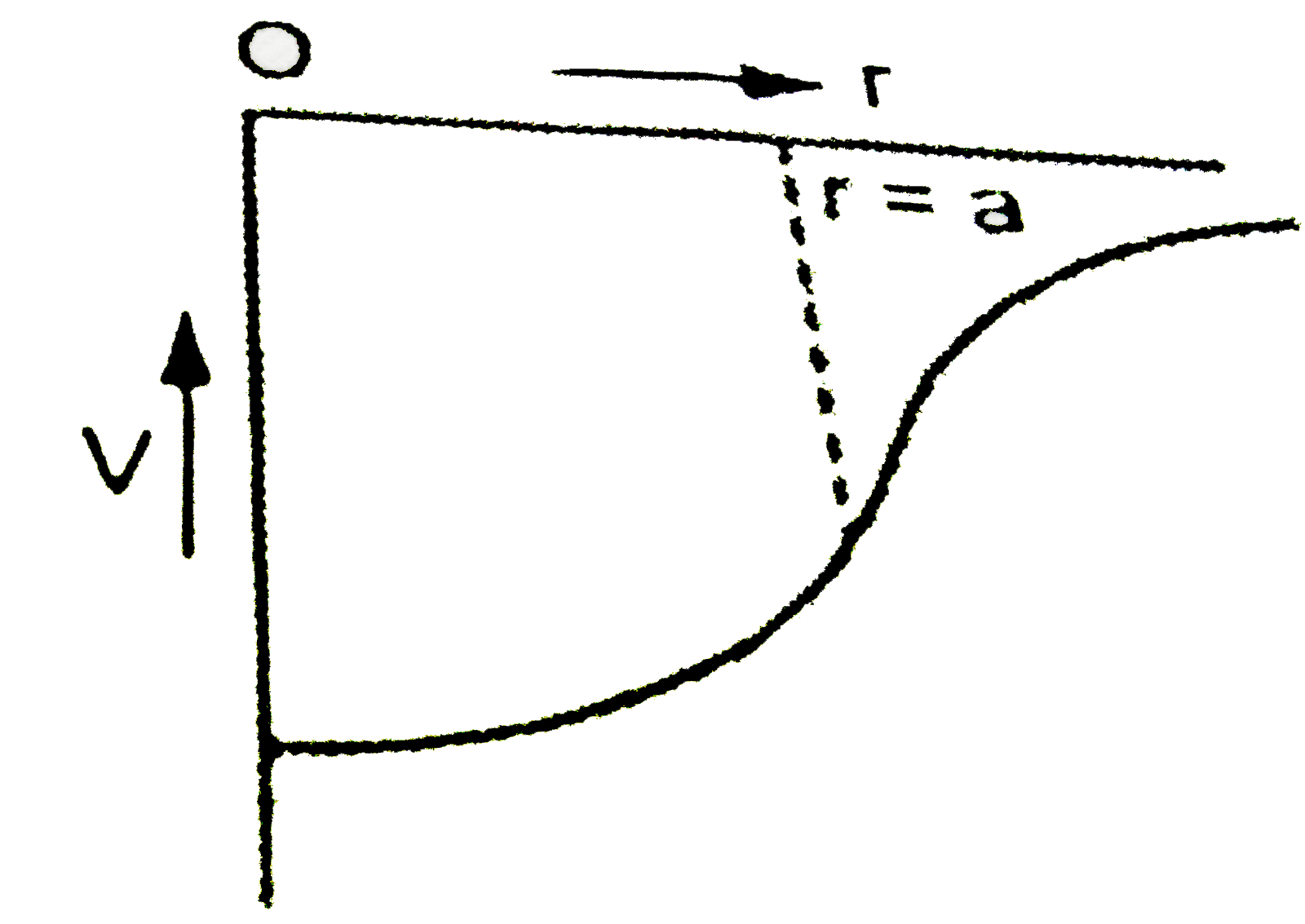
The correct Answer is:C
Step by step video, text & image solution for P is a point at a distance r from the centre of a solid sphere of radius a. The gravitational potential at P is V. IF V is plotted as a function of r, which is the correct curve ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionThe magnetic potential at a point at a distance r from its centre along its axis is V.The magnetic potential at a point at the distance 2 r will be
View Solution
Knowledge Check
- Question 1 - Select One
P is a point at a distance r from the centre of a spherical shell of mass M and radius a, where r<a. The gravitational potential at P is
A−GMrB−GMaC−GMra2D−GM(a−ra2) - Question 2 - Select One
The potential at a distance R/2 from the centre of a conducting sphere of radius R will be
A0BQ8πε0RCQ4πε0RDQ2πε0R - Question 3 - Select One
Potential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
AKQRBKQxCQx2DxQ
A cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphereView SolutionLet p=Qr3πR5 be the volume charge density at distance r from the centre for a a soild sphere of radius R and charge Q. The electric field at r=R2 from the centre will be
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View Solution_E01_035_Q01.png)
There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portional is M. What is the gravitational potential at centre?View Solution