A cavity of radius $R / 2$ is made inside a solid sphere of radius $R$ . The centre of the cavity is located at a distance $R / 2$ from the centre of the sphere. The gravitational force on a particle of a mass $' m'$ at a distance $R / 2$ from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here $g = G M / R^{2}$ , where $M$ is the mass of the solid sphere]

A

$\frac{m g}{2}$

B

$\frac{3 m g}{8}$

C

$\frac{m g}{16}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Gravitational field at mass $' m'$ due to full solid sphere
${\to E}_{1} = \frac{ρ \to r}{3 ε_{0}} = \frac{ρ R}{6 ε_{0}} ... ... ... ... [ε_{0} = \frac{1}{4 π G}]$
Gravitational field at mass $m$ due to cavity $(- ρ)$

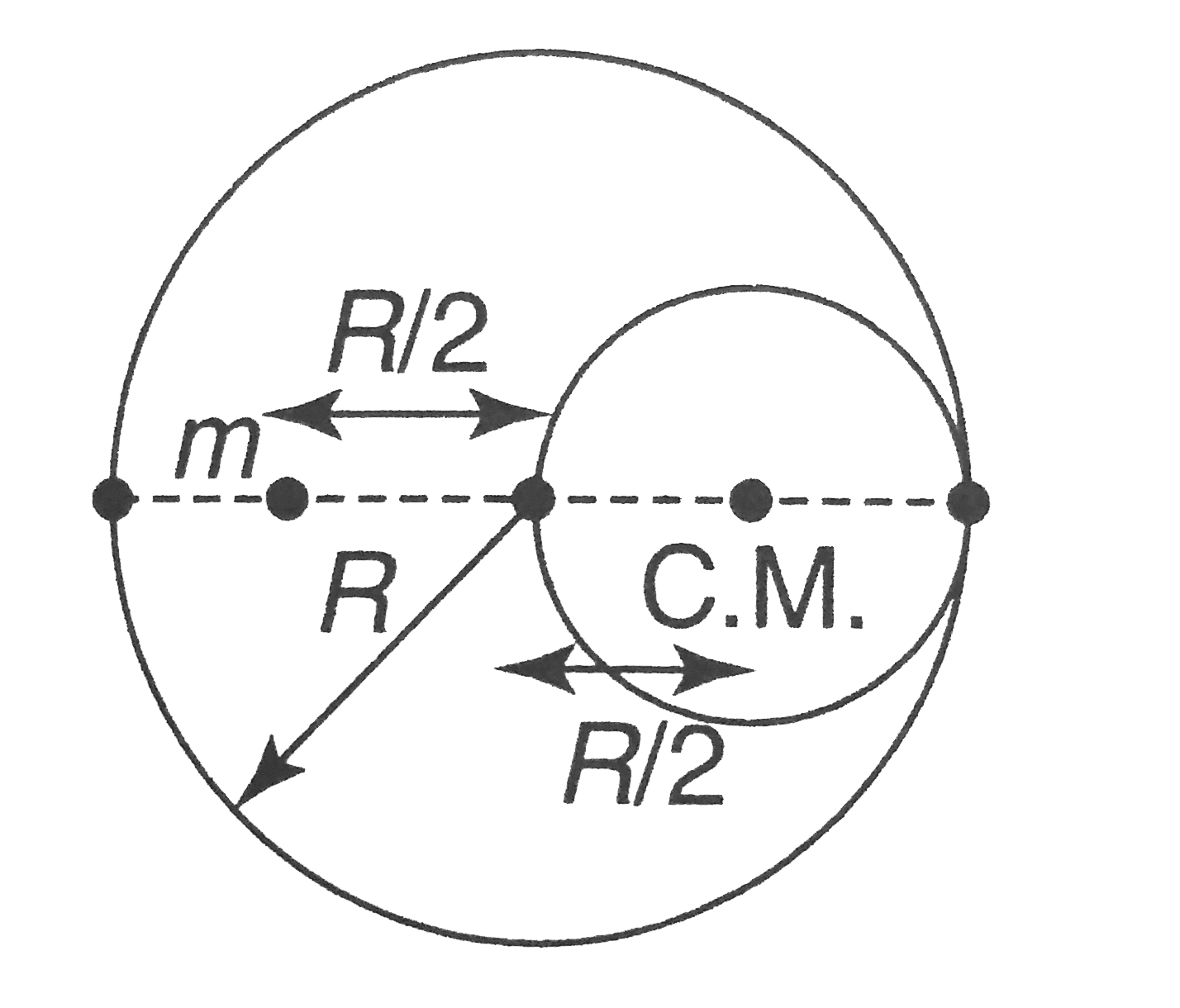
${\to E}_{2} = \frac{(- ρ) {(R / 2)}^{3}}{3 ε_{0} R^{2}} ... ... [\frac{ρ a^{3}}{3 ε_{0} r^{2}}]$
$= - \frac{(- ρ) R^{3}}{24 ε_{0} R^{2}} = - \frac{- ρ R}{24 ε_{0}}$
Net gravitational field
$\to E = {\to E}_{1} + {\to E}_{2} = \frac{ρ R}{6 ε_{0}} - \frac{ρ R}{24 ε_{0}} = \frac{ρ R}{8 ε_{0}}$
Net force on $' m' \to F = m \to E = \frac{m ρ R}{8 ε_{0}}$
Here, $ρ = \frac{M}{4 / 3 π R^{3}} & ε_{0} = \frac{1}{4 π G}$
Then $F = \frac{3 m g}{8}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A cavity of radius $R / 2$ is made inside a solid sphere of radius R. The centre of the cavity is located at a distance $R / 2$ from the centre of the sphere. The gravitational force on a particle of mass m at a distance $R / 2$ from the centre of the sphere on the line joining both the centre of the cavity)
[Here g $= (G M) / R^{2}$ , where M is the mass of the sphere
A $\frac{m g}{2}$
B $\frac{3 m g}{8}$
C $\frac{m g}{16}$
Dnone of these
Question 2 - Select One
The potential at a distance $R / 2$ from the centre of a conducting sphere of radius $R$ will be
A $0$
B $\frac{Q}{8 π ε_{0} R}$
C $\frac{Q}{4 π ε_{0} R}$
D $\frac{Q}{2 π ε_{0} R}$
Question 3 - Select One
The figure represents a solid uniform sphere of mass $M$ and radius $R$ . A spherical cavity of radius $r$ is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

Anon - uniform
Btowards the center of the cavity
Cdirectly proportional to $a$
DAll of these

A2Z-GRAVITATION-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile