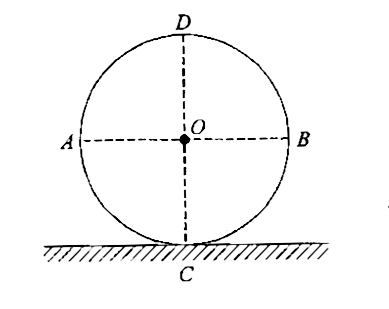
In a ring ABCD of radius r, the lower half ABC has mass m and the uppe

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

MISCELLANEOUS QUESTION 2BOOK - D MUKHERJEECHAPTER - MISCELLANEOUS QUESTION 2EXERCISE - Missellaneous Qns-2 (Assertion)
25 Videos
MISCELLANEOUS QUESTION 4BOOK - D MUKHERJEECHAPTER - MISCELLANEOUS QUESTION 4EXERCISE - Missellaneous Qns-4 (Matrix Matching Type)
9 Videos

Knowledge Check

In a ring ABCD of radius r, the lower half ABC has mass m and the upper half ADC has mass $2 m$ . In both parts, the masses are distributed evenly. The ring is initially at rest on a horizontal surface, as shown. O is the centre of the ring.

The ring is now folded along the diameter AC, such that the plane of the section ABC is normal to the plane of the section ADC. (The angle BOD $= 90^{\circ}$ ). It is then placed on a thin, fixed horizontal wire, ie.e, the diameter AC lies along the wire. The angle made by DO with the vertical will now be
A ${tan}^{- 1} (2 / 3)$
B ${tan}^{- 1} (1 / 2)$
C $30^{\circ}$
D $60^{\circ}$
In a ring ABCD of radius r, the lower half ABC has mass m and the upper half ADC has mass $2 m$ . In both parts, the masses are distributed evenly. The ring is initially at rest on a horizontal surface, as shown. O is the centre of the ring.

The ring is now pushed very slightly and begins to roll on the horizontal surface without slipping. When it has made half a rotation, i.e., B is vertically above D, its angualar velocity $ω$ will be given by (where $β = g / π r$ )
A $ω^{2} = 3 β / 2$
B $ω^{2} = 4 β / 3$
C $ω^{2} = 8 β / 5$
D $ω^{2} = 9 β / 4$
A uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is $V_{0}$ . The kinetic energy of the segment ABC is:

A $\frac{m V_{0}^{2}}{2} - \frac{m V_{0}^{2}}{π}$
B $\frac{m v_{0}^{2}}{2} + \frac{m v_{0}^{2}}{π}$
C $\frac{m v_{0}^{2}}{2}$
D $m v_{0}^{2}$